Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 10
Quando o corpo de está na posição mostrada, a mola de torção em é pré-tensionada de modo a exercer um momento de no sentido horário no corpo. Determine a força necessária para quebrar o contato em . Soluções completas para incluindo o efeito do peso e desprezando o peso.
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força necessária para quebrar o contato em em duas situações: incluindo os efeitos do peso e desprezando o peso. O primeiro passo aqui é determinar o momento causado pela mola e o peso do corpo de . Começando pela mola, ela está causando um momento sobre o ponto no sentido horário de:
E o peso do corpo pode ser facilmente obtido por:
Além da força e do momento causado pela mola, temos atuando no corpo o seu peso (que atua em algum ponto do eixo de simetria), as reações vertical e horizontal em e a força normal de contato. Para visualizar melhor o sistema de forças, vamos fazer o diagrama de corpo livre:
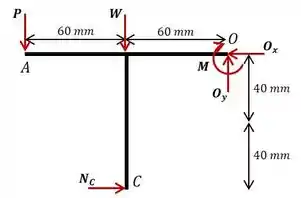
Passo 2
Até aqui apenas analisamos o problema. Agora bora trabalhar! O apoio em suporta apenas esforços de compressão, portanto, para quebrar o contato neste apoio, a força deve ser de tensão. Para manter o equilíbrio do corpo, o somatório de momentos em torno do ponto deve ser nulo, então:
Pelo item , devemos considerar o peso :
Uma vez que assumimos nos nossos cálculos que a reação é de compressão, para termos uma reação de tensão deve ser menor que zero.
Ou seja, a força mínima necessária para quebrar o contato em é:
Passo 3
Show de bola! Resolver o item agora ficou bem simples! Precisamos apenas voltar nessa equação:
E desconsiderar o peso, ou seja :
Novamente, a condição para ser de tensão:
Ou seja, a força mínima necessária para quebrar o contato em é:
Ufa! Essa já foi hein? Parece ser uma questão grande e difícil, mas fazendo aos poucos fica fácil né? Então partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 