Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 121
6.120 a 6.123 Para o dado estado plano de deformações usar o círculo de Mohr para determinar o estado de deformação associado aos eixos x'e y’, que foram girados de um ângulo , no sentido mostrado.
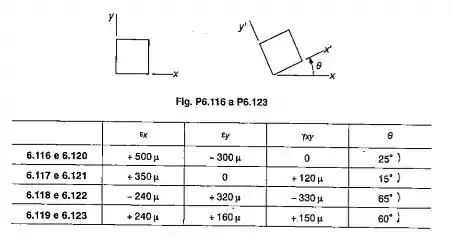
Passo 1
Fala aí, tá pronto pra mais essa?
Nosso objetivo aqui é encontrar o estado de deformação associado aos eixos x’ e y’, mas o que diabos isso quer dizer?
Quer dizer que devemos encontrar as deformações , e a deformação de cisalhamento daquele ponto. Pra isso a gente vai precisar usar o círculo de Mohr, então bora calcular os parâmetros dele. ATENÇÃO AOS SINAIS DAS DEFORMAÇÕES!
Começamos calculando o centro do círculo que nos será bem útil nos próximos cálculos:
E então o raio, que também é a deformação de cisalhamento máxima .
Passo 2
Aqui vamos encontrar o ângulo do estado de deformações, a gente pode fazer isso retirando do círculo de Mohr, um triângulo conhecido.
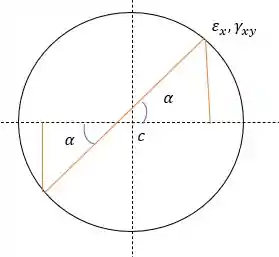
Sendo assim o ângulo inicial é:
Agora outro bizu, se o elemento girou horário, a gente gira anti-horário no círculo!
Nossa referência deve ser sempre o primeiro quadrante, considerando horário negativo e anti-horário como positivo, assim:
Passo 3
Enfim podemos calcular as deformações no ponto de interesse:
E a deformação de cisalhamento no ponto.