Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 132

As deformações específicas normais determinadas com o uso da roseta da figura, colada na superfície de um componente estrutural, são:

Determinar: (a) a orientação e a intensidade das deformações específicas nromais, no plano da roseta; (b) a máxima deformação de cisalhamento, no plano.

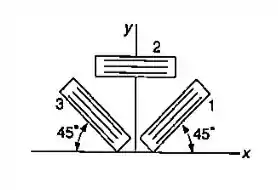
Passo 1

Esse problema nos fornece as deformações por meio da utilização da roseta, então a gente vai ter que achar as deformações através dos valores dados, primeiro vamos calcular os ângulos da roseta:

A partir daí a gente vai ter que achar as deformações . Vamos fazer isso no segundo passo.

Depois que achamos essas deformações podemos fazer o ciclo de Mohr e a brincadeira já ta no papo, partiu então!

Passo 2

As equações que vamos utilizar são da seguinte forma:

Daí é só substituir:

Para

Assim, temos o seguinte sistema:

Passo 3

Vamos resolver esse sistema:

Substituindo nas duas últimas equações:

Somando as duas equações:

Subtraindo as mesmas duas equações:

Assim temos as nossas deformações:

Passo 4

Vamos fazer então o ciclo de Mohr para deformações. Para isso a gente tem que lembrar como calcula a deformação específica normal média e o raio:

Perceba que é muito parecido com o ciclo de Mohr com as tensões mas aqui utilizamos:

que é a deformação específica normal.
que é a deformação angular.

utilizando os cálculos do passo 1:

Agora podemos desenhar o ciclo de Mohr:

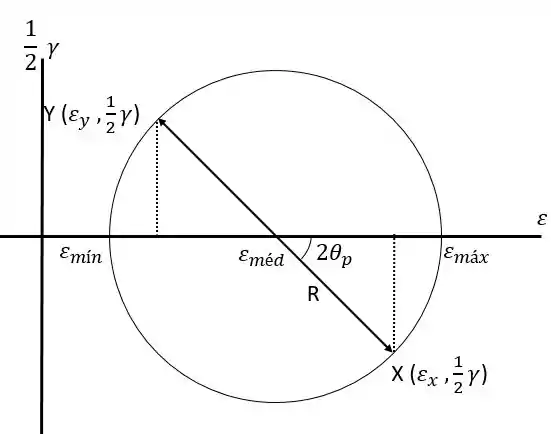
Passo 5

Com o círculo de Mohr a gente vai poder calcular a orientação das deformações específicas normais principais no plano da roseta. Para isso a gente tem que calcular o ângulo do ciclo de Mohr, que é dado, pela geometria do círculo como:

Passo 6

Para calcular a intensidade dessas deformações específicas normais principais temos que calcular e . Como já temos a média o o raio fica fácil:

Passo 7

A máxima deformação específica de cisalhamento no plano é obtida, também, pelo ciclo de Mohr e é igual ao raio a duas vezes o raio:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O quadrado deforma-se até chegar à posição mostrada pelas linhas tracejadas. Determine a deformação por cisalhamento em cada um de seus cantos A, B, C e D. O lado D’B’ permanece horizontal.

Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine as deformações normais médias ao longo do lado AB e das diagonais AC e DB.

A chapa retangular é submetida a deformação mostrada. Determine a deformação por cisalhamento média γ x y da chapa.

A chapa retangular é submetida à deformação mostrada pelas linhas tracejadas. Determine as deformações normais médias ao longo da diagonal AC e do lado AB.

A forma original da peça de borracha é retangular e ela é submetida à deformação mostrada pelas linhas tracejadas. Determine a deformação normal média ao longo da diagonal DB e do lado AD.