Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 129
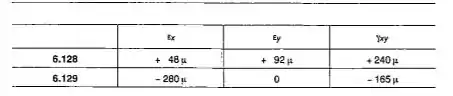
6.128 e 6.129 Em um ponto da superfície de uma placa fina foi determinado o estado de deformações. Sabendose que a superfície da placa está isenta de tensões e o coeficiente de Poisson é 0,30, determinar:(a) a orientação e a intensidade das deformações principais;(b) a máxima deformação específica de cisalhamento, no plano;(c) a máxima deformação específica de cisalhamento.
Passo 1
Oi, você por aqui? Já que veio, vamos fazer juntos mais essa?
Nosso objetivo aqui é encontrar a orientação das deformações normais principais em primeiro lugar.
Bom, traduzindo isso pra nossa língua, isso quer dizer que devemos usar o círculo de Mohr e encontrar , e pra isso a gente precisa dos parâmetros do círculo, ATENÇÃO AOS SINAIS DAS DEFORMAÇÕES!
Começamos calculando o centro do círculo que nos será bem útil nos próximos cálculos:
E então o raio, que também é a deformação de cisalhamento máxima .
Passo 2
Aqui vamos encontrar o ângulo do estado de deformações, a gente pode fazer isso retirando do círculo de Mohr, um triângulo conhecido.
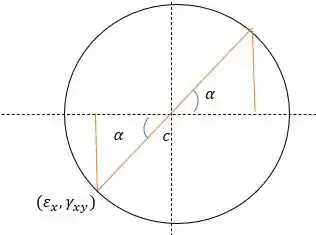
Sendo assim o ângulo inicial é:
E o ângulo desse plano é em relação ao primeiro quadrante:
Lembrando que dividimos por 2, pois se gira no círculo , giramos o elemento de pro sentido oposto.
Enfim podemos calcular as deformações principais e resolver nosso item a.
Orientação:
E a segunda deformação:
Que possui orientação:
Passo 3
Maneiro, resolvemos o primeiro item agora vamos calcular a deformação de cisalhamento máxima no plano que pode ser dada por:
Passo 4
Para o item c é pedido a máxima deformação específica de cisalhamento. E aqui que entra o coeficiente de Poisson, precisamos calcular a deformação específica e avaliar se é menor que a menor deformação principal ou maior que a maior deformação principal.
Nesse caso a máxima deformação específica é dada por:
Isso acontece quando as deformações e tem sinais opostos.
Resposta
a)
b)
c)