Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 137
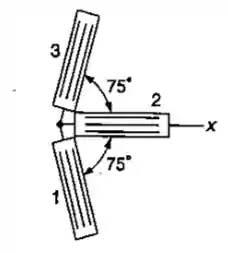
As deformações específicas normais determinadas com o uso da roseta da figura, colada na superfície de um componente estrutural, são:
Determinar: (a) as três deformações específicas normais no ponto onde as medidas foram feitas; (b) a máxima deformação de cisalhamento nesse ponto. Considere . (Nota: Lembrar que a superfície livre de um componente estrutural ou de máquina está em um estado plano de tensões.)
Passo 1
Esse problema nos fornece as deformações por meio da utilização da roseta, então a gente vai ter que achar as deformações através dos valores dados, primeiro vamos calcular os ângulos da roseta:
A partir daí a gente vai ter que achar as deformações . Vamos fazer isso no segundo passo.
Depois que achamos essas deformações podemos fazer o ciclo de Mohr e a brincadeira já ta no papo, partiu então!
Passo 2
As equações que vamos utilizar são da seguinte forma:
Daí é só substituir:
Para
Para
Para
Assim, temos o seguinte sistema:
Passo 3
Vamos resolver esse sistema substituindo nas duas últimas equações:
Somando as duas equações:
Subtraindo as mesmas duas equações:
Assim temos as nossas deformações:
Passo 4
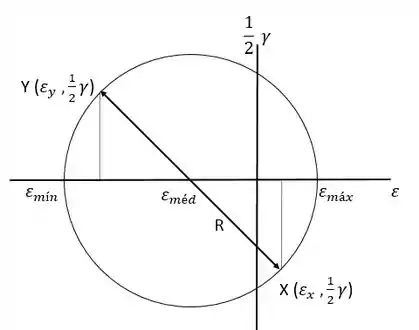
Vamos fazer então o ciclo de Mohr para deformações. Para isso a gente tem que lembrar como calcula a deformação específica normal média e o raio:
Perceba que é muito parecido com o ciclo de Mohr com as tensões mas aqui utilizamos:
- que é a deformação específica normal.
- que é a deformação angular.
utilizando os cálculos do passo 1:
E
Agora podemos desenhar o ciclo de Mohr:
Passo 5
Para calcular a intensidade dessas deformações específicas normais principais temos que calcular e . Como já temos a média o o raio fica fácil:
Passo 6
Para achar a última deformação normal específica a gente precisa lembrar de uma coisinha. Que quando um objeto deforma em um eixo ele irá deformar em outro eixo também. Isso depende do coeficiente de Poisson para calcular essa deformação vamos utilizar a seguinte equação:
Substituindo os valores calculados
Aqui vale uma observação do fato de existir um sinal negativo da própria fórmula. Isso acontece porque quando há uma contração num eixo o outro alonga. Pega uma massinha e amassa, ela não ficar mais longa? Ou seja, as deformações tem sinais contrários.
Passo 7
Se lembra que a máxima deformação específica de cisalhamento no plano é obtida, também, pelo ciclo de Mohr e é igual ao raio a duas vezes o raio:
Mas a gente não quer no plano, queremos no ponto! Logo o nosso ciclo de Mohr sofre uma leve mudança ao adicionarmos o termo
Perceba que o padrão:
Ainda é válido mas agora temos de pegar o círculo grandão, ou seja, a nova relação será:
Dessa forma:
Resposta
a)
b)