Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 131

Um quadrado A B C D de 15   m m de lado é riscado sobre a superfície de uma placa fina, quando a placa está sem carga. Depois da placa ser carregada, observou-se que o comprimento do lado A B diminui em 12   μ m , enquanto que o comprimento A D permaneceu inalterado e o ângulo D A B teve um decréscimo de 0,180 × 10 - 3   r a d . Sabendo-se que o coeficiente de Poisson é 1 / 3 , determinar: (a) a orientação e a intensidade das deformações específicas normais principais; (b) a máxima deformação específica de cisalhamento, no plano; (c) a máxima deformação específica de cisalhamento.

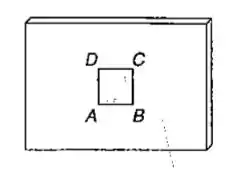
Passo 1

Vamos analisar os dados fornecidos pelas questão. Como foi dito que a variação do lado A B foi de 12   μ m vamos ter uma deformação específica normal de:

ε x = Δ L L 0

ε x = 12 × 10 - 6 15 × 10 - 3 = 0,8 × 10 - 3

Como não houve deformação em A D :

ε y = 0

Assim como uma deformação angular de:

γ x y = - 0,180 × 10 - 3   r a d

Sinal negativo porque houve um decréscimo.

A questão ainda forneceu um terceiro dado, que foi o coeficiente de Poisson:

ν = 1 3

Beleza, mas a gente calculou isso para que? Vamos utilizar esses cálculos para fazer o ciclo de Mohr para deformação, olha que legal kkk

Passo 2

Vamos fazer então o ciclo de Mohr para deformações. Para isso a gente tem que lembrar como calcula a deformação específica normal média e o raio:

ε m é d = ε x + ε y 2

R = ε x - ε y 2 2 + γ x y 2 2

Perceba que é muito parecido com o ciclo de Mohr com as tensões mas aqui utilizamos:

  • ε que é a deformação específica normal.
  • γ que é a deformação angular.

utilizando os cálculos do passo 1:

ε m é d = ε x + ε y 2

ε m é d = 0,8 × 10 - 3 + 0 2 = 0,4 × 10 - 3

E

R = 0,8 × 10 - 3 - 0 2 2 + - 0,180 × 10 - 3 2 2

R = 1,681 × 10 - 7

R = 0 , 041 × 10 - 3

Agora podemos desenhar o ciclo de Mohr, vale lembrar também que uma rotação no sentido horário é marcada acima do eixo horizontal, enquanto uma rotação no sentido anti-horário é marcada abaixo (neste nosso caso X será marcada abaixo já que roda no sentido anti-horário, porque o ângulo B A D diminui):

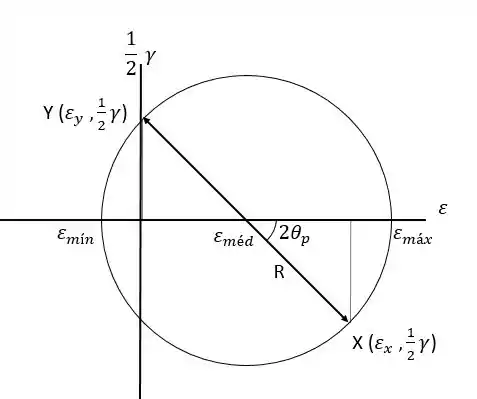
Passo 3

Com o círculo de Mohr a gente vai poder calcular a orientação das deformações específicas normais principais. Para isso a gente tem que calcular o ângulo 2 θ p do ciclo de Mohr, que é dado, pela geometria do círculo como:

t g 2 θ p = γ x y ε x - ε y

t g 2 θ p = - 0,180 × 10 - 3 0,8 × 10 - 3 - 0 = - 0,225

2 θ p = a r t g - 0,225

2 θ p = 12,68 °

θ p = 6,34 °

Então a orientação das deformações específicas normais principais são os ângulos:

θ a = 6,34 °

E

θ b = θ a + 90 ° = 96,34 °

Passo 4

Para calcular a intensidade dessas deformações específicas normais principais temos que calcular ε m á x e ε m í n . Como já temos a média o o raio fica fácil:

ε m á x = ε m é d + R

ε m á x = 0,8 × 10 - 3 + 0,041 × 10 - 3 = 0,841 × 10 - 3

ε m í n = 0,8 × 10 - 3 - 0,041 × 10 - 3 = 0,759 × 10 - 3

Passo 5

A máxima deformação específica de cisalhamento no plano γ m á x   ( n o   p l a n o ) é obtida, também, pelo ciclo de Mohr e é igual ao raio a duas vezes o raio:

1 2 γ m á x ( n o   p l a n o ) = R

γ m á x ( n o   p l a n o ) = 2 R

γ m á x ( n o   p l a n o ) = 2 ⋅ 0,041 × 10 - 3 = 0,082 × 10 - 3

Passo 6

Agora só falta a máxima deformação específica de cisalhamento ε c que é dada pelo coeficiente de Poisson da seguinte forma:

ε c = ν 1 - ν ⋅ ( ε a + ε b )

Onde ε a = ε m á x e ε b = ε m í n

ε c = 0,333 1 - 0,333 ⋅ ( 0,841 × 10 - 3 + 0,759 × 10 - 3 )

ε c = 0,499 ⋅ ( 1,6 × 10 - 3 )

ε c = 0,799 × 10 - 3

Resposta

a)

θ a = 6,34 °

θ b = 96,34 °

ε m á x = 0,841 × 10 - 3

ε m í n = 0,759 × 10 - 3

b) γ m á x ( n o   p l a n o ) = 0,082 × 10 - 3

c)

ε c = 0,799 × 10 - 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O material é distorcido até a posição, como mostra a figura. Determine a deformação normal média que ocorre ao longo das diagonais AD e CF.
O diâmetro de um balão de borracha cheio de ar é 150 mm. Se a pressão do ar em seu interior for aumentada até o diâmetro atingir 175 mm, determine a deformação normal média na borracha.
O cabeçote H está acoplado ao cilindro de um compressor por seis parafusos de aço. Se a força de aperto de cada parafuso for 4k N , determine a deformação normal nos parafusos. Cada um deles tem 5m m
3. As componentes do estado plano de deformação no ponto sobre a aba do pino são ϵ x = ( 200 × 10 - 6 ) , ϵ y = ( 180 × 10 - 6 ) e γ x y = ( - 300 × 10 - 6 ) . Use as equações de transformação da defo
As componentes do estado plano de deformação no ponto da aba da bequilha são ϵ x = ( - 400 × 10 - 6 ) , ϵ y = ( 860 × 10 - 6 ) e γ x y = ( 375 × 10 - 6 ) . Use as equações de transformação da deformaç