Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 30

6/30) A barra uniforme com centro de massa em G é suportada pelas cavilhas A e B que estão presas à roda . Se o coeficiente de atrito entre a barra e as cavilhas é μ , determine o ângulo θ que a roda pode ser lentamente girada em torno de seu eixo horizontal passando por O , começando a partir da posição mostrada , antes que a barra comece a deslizar . Despreze o diâmetro da barra comparado com as outras dimensões .

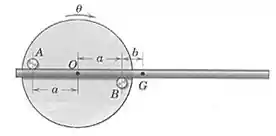
Passo 1

Então galera , sejam A e B forças aplicadas nos pontos indicados na figura do enunciado . Com isso definido , devemos primeiramente aplicar a equação de equilíbrio em relação ao centro de massa da barra :

∑ M G = 0   : A 2 a + b - B b = 0  

Dessa forma ,

B A = 2 a + b b

Agora aplicando a equação de equilíbrio em relação ao eixo x , obtemos que :

∑ F x = 0   : B - A sen ⁡ θ - μ A + B cos ⁡ θ = 0

Achamos assim uma relação para θ na qual :

tan ⁡ θ = μ A + B B - A = μ 1 + B A B A - 1

Passo 2

Bom pessoal , agora substituindo B A da relação encontrada para θ no passo anterior pelo valor que havia sido obtido anteriormente , achamos que :

tan ⁡ θ = μ 1 + 2 a + b b 2 a + b b - 1

Logo ,

θ = tan - 1 ⁡ μ a + b a

Resposta

θ = tan - 1 ⁡ μ a + b a

E aí , Topam resolver mais questões com a gente ?

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força P mínima para impedir que a barra A B de 30 k g deslize. A superfície de contato em B é lisa, enquanto o coeficiente de atrito estático entre a barra e a parede em A é μ s = 0,2 .
Se cada caixa pesa 75k g , determine a menor força horizontal P que o homem precisa exercer na caixa de cima a fim de causar movimento. O coeficiente de atrito estático entre as caixas é μ s = 0,5 , e
O carpinteiro empurra lentamente a tábua uniforme horizontalmente sobre o topo do cavalete. A tábua tem um peso uniforme de 50N / m , e o cavalete tem um peso de 75N e centro de gravidade em G . Deter
O carpinteiro empurra lentamente a tábua uniforme horizontalmente sobre o topo do cavalete. A tábua tem um peso uniforme de 50N / m , e o cavalete tem um peso de 75N e centro de gravidade em G . Deter
Se cada caixa pesa 75k g , determine a menor força horizontal P que o homem precisa exercer na caixa de cima a fim de causar movimento. O coeficiente de atrito estático entre as caixas é μ s = 0 , 6 5