Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 57

Se cada caixa pesa , determine a menor força horizontal que o homem precisa exercer na caixa de cima a fim de causar movimento. O coeficiente de atrito estático entre as caixas é , e o coeficiente de atrito estático entre a caixa e o piso .

Passo 1

O problema pede que descubra a menor força horizontal para causar movimento.

Beleza, a gente vai começar fazendo um diagraminha de corpo livre com o peso da garota:

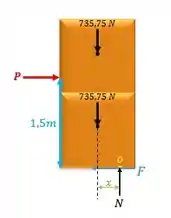
A força de atrito no solo que que tá de azul é:

Passo 2

Agora, para a gente calcular calcular a força de atrito a gente tem que calcular a Normal, que é a reação do solo, então vem comigo analisar as forças verticais:

Então agora sim, a gente consegue encontrar a força de atrito no solo:

Passo 3

Bom, então para acontecer o movimento a força só precisa vencer o atrito, logo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o coeficiente mínimo de atrito estático μ s que permitirá que o tambor com cubo interno fixo seja enrolado na inclinação de 15 ° a uma velocidade constante sem escorregar. Quais são os valor

Os coeficientes de atrito estático e cinético entre o bloco de 100k g e o plano inclinado são 0,30 e 0,20 , respectivamente. Determine a a força de atrito F atuando no bloco quando P é aplicado com um

A ilustração mostra o projeto de um dispositivo de travamento do tipo came, que, na presença de atrito suficiente, limita o movimento do corpo B para ser apenas para a esquerda; o movimento para a dir

A extremidade superior da barra do Prob. 15/6 agora está encostado a uma parede não vertical. Determine o valor mínimo do ângulo θ para o qual o equilíbrio é possível para μ s =0,25 e para μ s =0,50 .

A barra esbelta uniforme tem um rolo ideal em sua extremidade superior A. Se o coeficiente de atrito estático em B for μ s =0,25 , determine o ângulo mínimo θ para o qual o equilíbrio é possível. Repi