Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 143
143- A viga sustenta uma carga unitária uniforme . Determine a posição dos dois apoios de modo a minimizar o momento fletor máximo na viga. Especifique o valor de .
Passo 1
A força resultante pela carga retangular na viga é de:
E como os dois apoios estão simétricas ao meio da barra nós temos nas reações duas forças iguais a:
Onde o apoio da esquerda chamei de o apoio da esquerda e o apoio da direita.
Então podemos escrever a viga da seguinte forma:
Passo 2
Dessa forma conseguimos determinar o diagrama cortante da viga analisando os retângulos marcados por números:
Para o retângulo 1 que analisa a seção indo de até temos uma cortante igual a:
Logo a cortante nessa seção vale :
Logo o momento fletor no final dessa seção valerá:
Para o intervalo retângulo temos uma similaridade a equação da cortante vendo da direita pra esquerda é de:
E o momento fletor em será:
Logo no retângulo 1 e 3 temos o mesmo gráfico de momento, porém a cortante tem sinais trocados.
Olhando para o primeiro apoio, nós temos uma cortante vinda da seção 1 igual a e se somada com a reação nesse primeiro apoio nós teremos então uma cortante inicial igual a:
Passo 3
No segundo apoio vindo pela seção temos um valor de cortante igual a:
Porém ao final da seção o apoio tem uma contribuição vinda do apoio igual a então ao final da seção 2 a seção entrega uma cortante igual a :
O que nos dá um diagrama de cortante igual a:
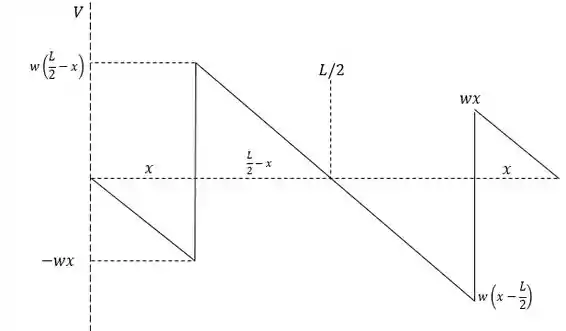
Passo 4
Calcular a equação da cortante na seção seria muito trabalhoso e a chance de errar seria gigantesca, então para calcular o momento total na seção vamos calcular a área dos dois triângulos que compõem a cortante no mesmo.
Área do primeiro triângulo:
Porém temos que somar com a contribuição de momento da seção anterior se quisermos saber o momento máximo:
Como sabemos que a integral de uma reta decrescente dá uma parábola com concavidade para baixo então temos o seguinte diagrama de momento fletor.
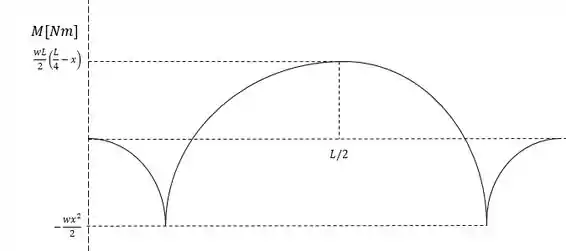
Agora podemos ver que quanto maior o valor de maior o momento fletor nas seções e e enquanto isso o momento fletor na seção tende a diminuir, se aumentarmos muito o intervalo o momento fletor nas seções e passam a ser o momento máximo. Logo a melhor maneira de diminuir ao máximo o máximo momento é igualando essas duas equações, o que nos dá:
Resolvendo essa equação do segundo grau temos:
Como não podemos ter uma valor de negativo então nosso que vai fazer com que o momento seja mínimo será:
Substituindo esse valor de em qualquer uma das equações de momento fletor temos: