Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 53
O carpinteiro empurra lentamente a tábua uniforme horizontalmente sobre o topo do cavalete. A tábua tem um peso uniforme de , e o cavalete tem um peso de e centro de gravidade em . Determine se o cavalete permanecerá na posição, deslizará ou tombará se tábua for empurrada para frente quando . Os coeficientes de atrito estático são indicados na figura.
Passo 1
O problema pede que descubra se o cavalete deslizará, tombará ou ficará imovél.
Beleza, a gente vai começar analisando o momento da parte da tábua antes do cavalete:
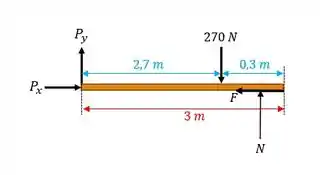
O momento fica:
Então vamos usar como se fosse igual ao atrito máximo entre a tábua e o cavalete:
Passo 2
Agora, para o cavelete não deslizar a força não pode ultrapassar a de atrito estático máxima:
E para o cavalete não tombar o somatório do momento deve ser zero:
Passo 3
Calma, tá quase acabando, só o que a gente precisa saber é interpretar o que a gente tem, é mais fácil do que parece.
Bom, a força máxima que pode ser aplicada antes de da tábua deslizar é , então a gente vê primeiro se com essa força o cavalete desliza no chão a força que ele pode receber antes de deslizar é , e a força máxima que ele pode receber antes de tombar é .
E como a força necessária para deslizar é menor que para tombar, ele vai deslizar.
Resposta
O cavalete irá deslizar.