Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 64
64. O poste de uma linha de transmissão elétrica está sujeito a duas forças do cabo de , situadas em um plano paralelo ao plano . Se a tração no fio tirante é , determine as componentes da reação na base fixa do poste.
Passo 1
Fala ai galerinha do RespondeAí, tudo belezinha? Bora lá resolver esse exercício aqui:
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso é uma base fixa e segundo a tabela do capítulo , seção , esse tipo de conexão exerce forças nas direções e momentos nas mesmas direções.
Abaixo temos o diagrama de corpo livre da situação.
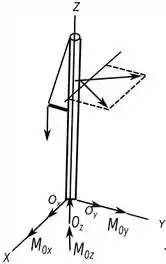
Agora para determinar vamos usar as equações de equilíbrio.
Passo 2
Vamos começar com as equações de equilíbrio referente as forças. Temos:
No eixo :
Logo:
Já para o eixo , teremos que:
Passo 3
Agora vamos com as equações de equilíbrio referente aos momentos. No eixo temos:
Tal que:
Logo isolando :
Agora fazendo o mesmo para o eixo :
De forma que:
E por fim para o eixo :
Portanto: