65. A chave mostrada na figura é usada para girar o eixo. Um pino é fixado no furo em A , enquanto noutro ponto, sem atrito, apoia sobre o eixo em B . Se a força P de 240N é exercida na chave em D, encontre as reações em A e B .

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 65

65. A chave mostrada na figura é usada para girar o eixo. Um pino é fixado no furo em , enquanto noutro ponto, sem atrito, apoia sobre o eixo em . Se a força de é exercida na chave em D, encontre as reações em e .

Passo 1

Vamos resolver esse exercício a base de trigonometria, mas para isso teremos que achar as reações trigonométricas para isso. Então vamos analisar o seguinte diagrama de movimento.

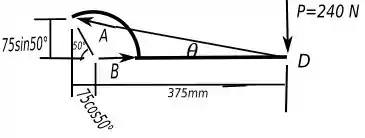
Olhando esse diagrama podemos tirar o seguinte esquema, que vai nos facilitar a vida.

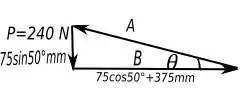
Então podemos determinar o ângulo com uma trigonometria bem maneira, assim:

Tendo o valor de podemos achar a força que atua em e a força que atua em , através das seguintes relações trigonométricas:

Passo 2

Vamos determinar a força que atua em .

Passo 3

Agora vamos determinar a força em .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma tora de madeira pesando 3600 N é presa por uma tenaz como mostrado na figura. Determine as forças exercidas em E e F na garra D E F .

A tenaz mostrada na figura é usada para aplicar uma força total para cima de 45 k N no tampão da tubulação. Determine as forças exercidas em D e F na garra A D F .

Se a chave mostrada é adicionada à tenaz do problema 6.143 e uma força vertical única é aplicada em G , determine as forças exercidas em D e F na garra A D F .

Ao usar o cortador de parafusos mostrado na figura, um operário aplica duas forças de 300 N aos cabos da ferramenta. Determine a intensidade das forças exercidas pelo cortador no parafuso.

Determine a intensidade das forças de aperto produzidas quando duas forças de 300 N são aplicadas tal como mostra a figura.