Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 141

Uma tora de madeira pesando 3600 N é presa por uma tenaz como mostrado na figura. Determine as forças exercidas em E e F na garra D E F .

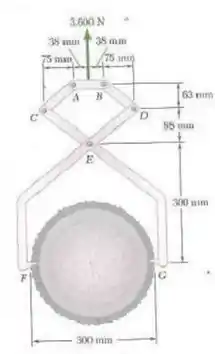
Passo 1

Para analisarmos o problema, façamos primeiramente o diagrama de corpo livre dele dado por

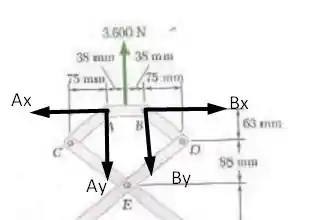
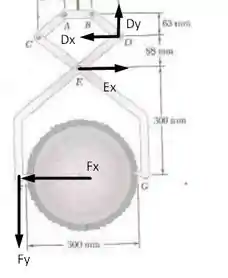
Assim, utilizando a simetria do problema vamos ter

A y = B y = 1.8 k N

A x = B x = 75 63 ⋅ 1800 = 2.143 k N

D = - B → D x = B x = 2.143 k N   e   D y = B y = 1.8 k N

Agora, analisando a barra F E D teremos e aplicando as condições de equilíbrio vamos ter

∑ M f = 0 → 260 m m ⋅ 1.8 k N + 2.143 k N ⋅ 385 m m - E x ⋅ 300 m m = 0

→ E x = E = 4.31 k N

∑ F x = 0 →   - 2.143 k N + 4.31 k N - F x = 0 → F x = 2.167 k N

∑ F y = 0   → 1.8 k N - F y = 0 → 1.8 k N

Resposta

E = 4,31 k N   e   F x = 2.167 k N   e   F y = 1.8 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O dobrador de tubos consiste em duas polias ranhuradas montadas e livres para girar em uma estrutura fixa. O tubo é dobrado na forma mostrada por uma força P = 300N . Calcule as forças suportadas pelo
A parte lombar da coluna vertebral humana suporta todo o peso da parte superior do tronco e a carga de força que lhe é imposta. Consideramos aqui o disco (sombreado em vermelho) entre a vértebra infer
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.1. Determine as componentes horizontal e vertical da reação dos apoios. Despreze a espessura da viga.
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.5. A haste de 25 kg possui centro de massa em G. Se ela é sustentada por uma cavilha lisa em C, um rolete em A e a corda
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.6. Determine as reações nos pontos de contato lisos A, B e C na alavanca.