Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 68
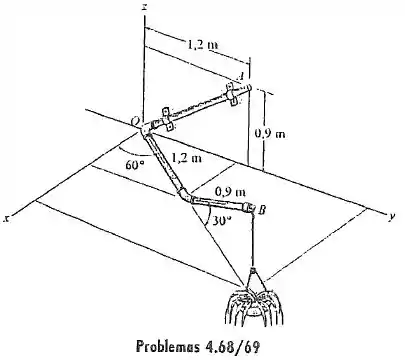
A tubulação é fixa na parede pelas duas abraçadeiras. Se o vaso de planta possui um peso , determine a intensidade do momento produzido pelo peso em relação ao eixo .
Passo 1
Para determinarmos o momento produzido peso da planta, pensaremos da seguinte forma:
Os pontos e formarão um vetor , vetor este que será nosso eixo de rotação do momento, Note que teremos que calculo o vetor unitário de . Pois, apenas desejamos a direção e sentido do eixo de rotação. Que chamaremos de .
A partir deste eixo , teremos os vetores entre os pontos e B, o vetor entre os pontos e que serão os nossos vetores comprimento do nosso momento.
Portanto para determinar o momento teremos uma multiplicação entre o eixo, vetor comprimento e peso.
Resumidamente teremos a seguinte equação:
Onde representam as componentes do vetor unitário definido pelo eixo que passa pelos pontos e .
representam as coordenadas do vetor posição definido a partir de um ponto qualquer do eixo até um ponto qualquer da linha de atuação da força.
Passo 2
Vamos determinar o vetor unitário , para isto vamos determinar o vetor :
Olhando para figura, podemos afirmar que as coordenadas do ponto é a seguinte:
E as coordenadas do ponto , fica o seguinte:
Considerando o ponto como inicial e o ponto como final do nosso vetor pode ser determinado, pela seguinte definição:
Substituindo os pontos, temos:
Para determinar o vetor unitário, temos que obter módulo do vetor , logo:
Calculando o vetor unitário , temos:
Passo 3
Temos o vetor unitário , precisamos determinar o nosso vetor comprimento .
Esse vetor comprimento, precisa ser partindo de um ponto do eixo até um ponto na linha de atuação da força. Escolhi o ponto por que ele está na origem e será fácil de calcular!
Para um ponto na linha de atuação da força, se dermos uma olhada no desenho...
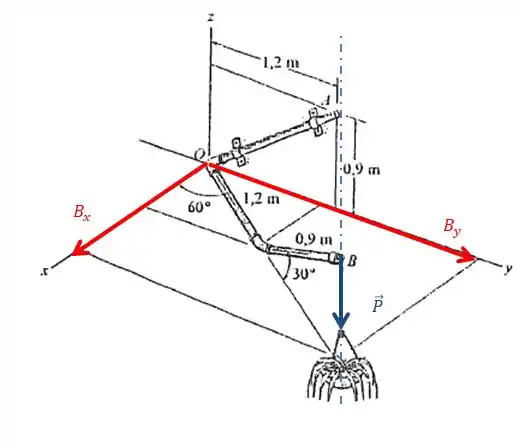
Vemos que a linha de atuação da força peso, é uma linha vertical no eixo , por isso, eu posso encontrar as coordenadas e do ponto , mas não preciso me preocupar com a coordenada , pois em qualquer valor dela, vou ter um ponto em cima da linha de atuação da força.Para facilitar nossas contas, vou considerar um ponto com coordenada .
Agora, precisamos de e !
Primeiro, precisamos saber quanto vale a projeção do cano inclinado de sobre o plano .
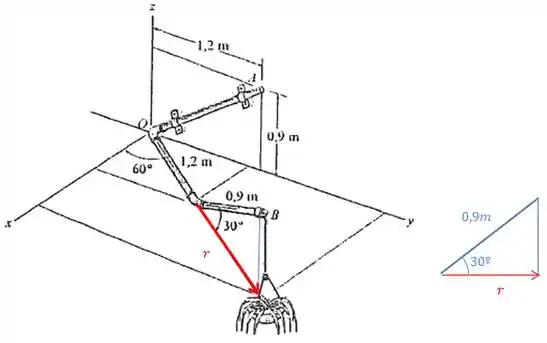
Pelo triângulo que é formado, vemos que essa projeção vale:
Vamos dar uma olhada nesse cano, olhando de cima, vendo apenas o plano e .
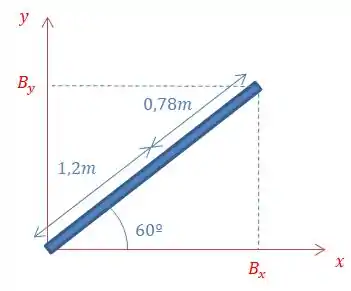
Daí, tiramos que:
Considerando o ponto como inicial e o ponto como final do nosso vetor pode ser determinado, pela seguinte definição:
Substituindo os pontos, temos:
Passo 4
Bem estamos prontos para efetuar o cálculo do momento:
Para substituir todo mundo, falta apenas indicar qual é a força. Aqui temos uma força peso, portanto, será:
Substituindo nossos cálculos, temos:
Executando o determinante, temos:
Sendo assim, o momento gerado por essa força ao redor do eixo é de !