Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas fundamentais - Ex. 13

13. Determine a velocidade angular da barra e a velocidade do ponto C no instante mostrado.

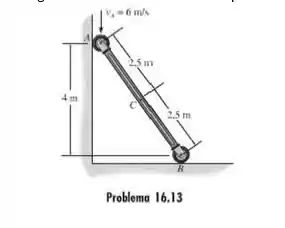
Passo 1

O esboço da figura que mostra o centro instantâneo da haste e nos ajudará na resolução é representado por:

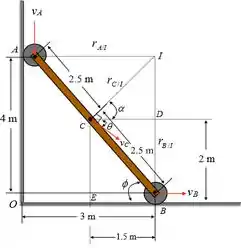
Temos que o calculo da distância do centro instantâneo até A é o seguinte:

r A I 2 = O B 2 - O A 2

r A / B = 3 m

Considere a expressão para a velocidade angular no ponto da A seguinte maneira:

ω A B = v A r A / I

ω A B = 6 3

= 2   r a d / s

Portanto, a velocidade angular da haste  ω A B   é  2   r a d / s .

Passo 2

Calcule o comprimento EB a partir do princípio dos triângulos semelhantes dos triângulos ∆ C E B  e  ∆ A O B :

E B C B = O B A B

E B = 3 5 × 2,5

= 1,5   m

Considere a seguinte relação da figura:

C E = D B

Calcule o comprimento da BD seguinte maneira:

B D = B C 2 - E B 2

B D = 2,5 2 - 1,5 2

= 2   m

Calcule o ID do comprimento da seguinte maneira:

I D = I B - B D

= A O - B D

= 4 - 2

= 2   m

Calcule a distância do centro instantâneo até C o seguinte:

r C I 2 = C D 2 + I D 2

r C / I = 2,5   m

Calcule o ângulo inclinado da haste com o OB da seguinte maneira:

sin ⁡ ϕ = O A A B

sin ⁡ ϕ = 4 5

sin ⁡ ϕ = 0,8

ϕ = 53,13 °

Calcule a velocidade no ponto C usando a seguinte relação:

v C = ω A B r C I

= 2 × 2,5

= 5   m / s

Portanto, a velocidade no ponto  v C   é  5   m / s .

Saca só, neste caso tivemos que fazer alguns cálculos antes para depois substituir os valores na equação anterior e encontrar aquilo que o enunciado nos propõe.

Passo 3

Calcule o ângulo  α usando a seguinte relação:

α = tan - 1 ⁡ I D C D

α = tan - 1 ⁡ 2 1,5

= 53,13 °

Calcule o ângulo  θ   para o qual o direcionamento é o seguinte:

θ = 90 ° - α

= 36,87 °

Portanto, a velocidade é direcionada em um ângulo  θ de  36,87 ° .

Resposta

ω A B = 2   r a d / s

v C = 5   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

51. Se o cilindro hidráulico AB está se estendendo a uma taxa constante de 0,3 m/s, determine a velocidade angular do basculante no instante θ = 30 ° .
43. A extremidade A da barra se desloca para a esquerda com uma velocidade constante v A . Determine a velocidade angular ω e aceleração angular a da barra como uma função da posição x.
44. Determine a velocidade e aceleração da placa no instante θ = 30 ° , se nesse instante o came circular está girando em torno do ponto fixo O com uma velocidade angular ω = 4r a d / s e um aceleraçã
12. A extremidade A da barra de ligação tem uma velocidade v A = 3m / s . Determine a velocidade do pino em B nesse instante. O pino está restrito a se deslocar ao longo da ranhura.