Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 68
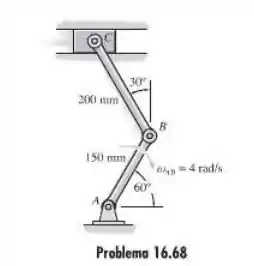
68. Se a barra AB tem uma velocidade angular AB=4 rad/s, determine a velocidade do bloco deslizante C no instante mostrado.
Passo 1
A velocidade angular da barra é expressa como
Nesse sentido, temos
A partir da equação da velocidade, temos
O vetor de posição direcionado de B para C é expresso como
Passo 2
Nós temos e
Para a barra BC, temos
Nesse sentido, temos
Ao substituir os valores dos parâmetros na equação da velocidade obtida no passo 1, temos
Atenção ao sentido dos vetores ao realizar o produto vetorial.
Separando as componentes a gente tem:
Passo 3
Ao equacionar os coeficientes em j, obtemos
Ao equacionar os em i, pois agora já obtemos o que tava faltando para equacionar esse, obtemos de (2)
A velocidade do bloco deslizante C no instante mostrado é .
Resposta
Exercícios de Livros Relacionados
Determine a velocidade angular do segmento BC e a velocidade do pistão C no instante mostrado.
Determine a velocidade angular dos segmentos BC e CD no instante mostrado.
Se a engrenagem do cubo H e a engrenagem interna R têm velocidades angulares ω H = 5r a d / s e ω R = 20r a d / s , respectivamente, determine a velocidade angular ω s da engrenagem de dentes retos S
Para a roda de Genebra do Prob. 5/56, mostrada aqui novamente, escreva a expressão para a velocidade angular ω 2 da roda ranhurada C durante o acoplamento do pino P e represente graficamente ω 2 para
O braço ranhurado OB oscila em torno da vertical pela ação da manivela rotativa CA com 125 mm de comprimento, onde o pino A se acopla à ranhura. Para uma velocidade constante N = 120r p m da manivela