Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 77
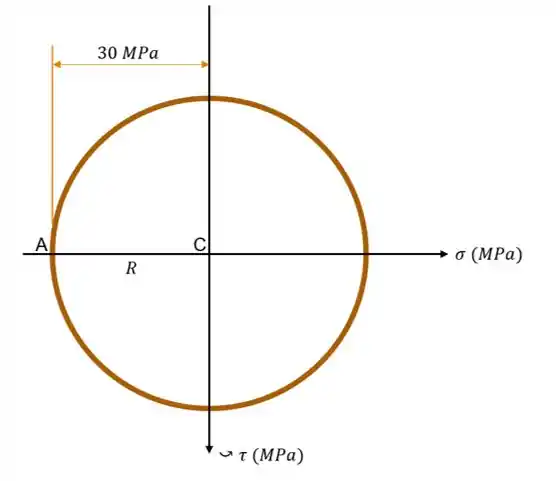
77. Obtenha o círculo de Mohr que descreve cada um dos seguintes estados de tensão.
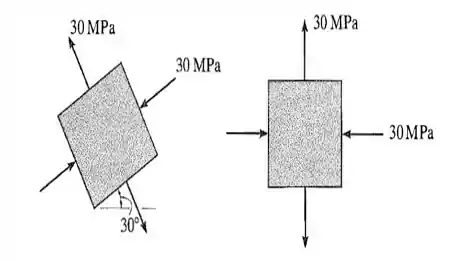
Passo 1
Como pode-se ver na figura, os dois elementos tem as mesmas tensões. Que sorte a nossa, porque só vamos precisar construir um círculo para os dois casos:
Da figura do enunciado, tiramos que:
A primeira coisa que temos que fazer para construir nosso círculo é determinar a tensão média , através da fórmula abaixo:
E substituindo os valores numéricos correspondentes, chegamos à:
Depois, o próximo passo é achar o raio que nada mais nada menos, é a tensão máxima de cisalhamento , a qual é dada por:
Trocando os valores de cada variável, obtemos nossa tensão máxima como:
Passo 2
Obtido a tensão média e a tensão de cisalhamento máxima, já temos o que precisamos para construir nosso círculo:
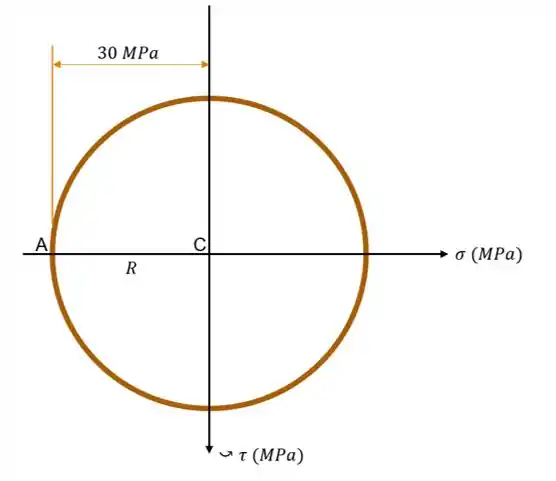
Resposta
