Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 57

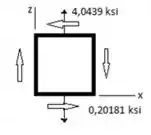
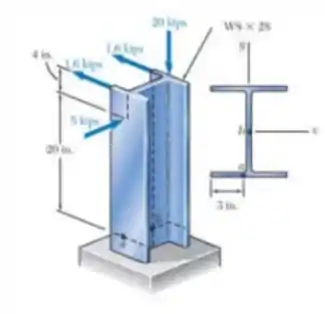
8.57 Quatro forças são aplicadas a um perfil de aço laminado W8x28, conforme mostra a figura. Determine as tensões principais e a tensão de cisalhamento máxima no ponto a.

Passo 1

Calcular forças e pares na seção contendo ponto de interesse.

P = 28 k i p s     V x = - 3,2 k i p s         V y = 5 k i p s  

M x = - 20 5 - 4,03 20 = - 180,6 k i p ∙ i n .

M y = - 20 + 4 3,2 = - 76,8 k i p ∙ i n .

Passo 2

Propriedades da seção:

A = 8,24 i n 4         d = 8,06 i n .       b f = 6,54 i n .         t f = 0,465 i n .

t w = 0,285 i n .           I x = 98,0 i n 4           I y = 21,7 i n 4

Ponto a: x a = - 6,54 2 + 3 = - 0,27 i n .         y a = - 8,06 2 = - 4,03 i n .

σ a = - P A + M x y a I x - M y x a I y = - 20 8.24 + - 180,6 - 4,03 98,0 - - 76,8 - 0,27 21,7 = - 2,4272 + 7,4267 - 0,95558 = 4,0439 k s i

Passo 3

Tensão de cisalhamento causada em a por V x :

A = 3 0,465 = 1,395 i n 2

x - = - 6,54 2 + 3 2 = - 1,77 i n .

Q = - A x - = 2,4692 i n 3

τ x z = V x Q I y t = - 3,2 2,4692 21,7 0,465 = - 0,78306 k s i

Tensão de cisalhamento no ponto a por V y :

A = 3 0,465 = 1,395 i n 2

y - = - 8,06 2 + 0,465 2 = - 3,7975 i n .

Q = - A y - = 5,2975 i n 3

τ x z = V y Q I x t = 5 6,2975 98,0 0,465 = 0,58125 k s i

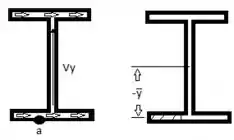
Passo 4

Tensão de cisalhamento combinada:

- 0,78306 + 0,58125 = 0,20181 k s i

σ a v e = 4,0439 + 0 2 = 2,0220 k s i

R 40,0439 - 0 2 2 + 02,0181 2 = 2,0320 k s i

σ M A X = σ a v e + R                   σ M A X = 4,05 k s i

σ M I N = σ - R                   σ M I N = - 0,010 k s i

τ M A X = R                 τ M A X = 2,03 k s

Resposta

σ M A X = σ a v e + R                   σ M A X = 4,05 k s i

σ M I N = σ - R                   σ M I N = - 0,010 k s i

τ M A X = R                 τ M A X = 2,03 k s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tampa do tanque cilíndrico é parafusada ao tanque ao longo das abas. O tanque tem diâmetro interno de 1,5 m e espessura da parede de 18 mm. Considerando que a maior tensão normal não deve ultrapassa
O apoio tem seção transversal circular, cujo raio aumenta linearmente com a profundidade. Se for submetido à carga de compressão P, determine as tensões normais máxima e mínima que agem no material.
O olhal está sujeito à força de 250 N. Determine as tensões de tração e compressão máxima na seção a-a. A seção transversal é circular e tem 6 mm de diâmetro. Use a fórmula da viga curva para calcular
A tampa do tanque cilíndrico é parafusada ao tanque ao longo das abas. O tanque tem diâmetro interno de 1,5 m, e a espessura da parede é 18 mm. Se a pressão no interior do tanque for p = 1,20 MPa, det
O parafuso de prensa é composto pelos elementos estruturais AB e AC conectados por um pino em A. Se a força de compressão em C e B for 180 N, determine o estado de tensão no ponto F e indique os resul