Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 29

O eixo cheio AE gira a 600   r p m e transmite 60   h p do motor M para as máquinas-ferramentas acopladas às engrenagens G e H .Sabendo que τ a d m   = 55,2   M P a e que 40   h p são transmitidos pela engrenagens G e 20   h p são transmitidos pela engrenagem H, determine o menor diâmetro admissível para o eixo AE.

Passo 1

E aí gurizada, vamos começar nosso cálculo? Vamos começar pelo esboço do diagrama de corpo livre, vem comigo ;)

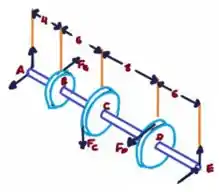
Temos que:

60   h p = ( 60 ) ( 6600 ) = 396 × 10 3   i n / l b / s e g

f = 600   r p m 60   s e g / m i n -   10   H z

Passo 2

Força na engrenagem B:

T B = P 2 π f = 396 × 10 3 2 π ( 10 ) = 6302,5   l b / i n

Forças nas engrenagens C e D:

T C ´ = 40 60 T B = 4201,7   l b / i n

T D = 20 60 T B = 2100,8   l b / i n

Passo 3

Forças no eixo:

A B : T A B = 0 B C : T B C = 6302.5   l b / i n

C D : T C D = 2100.8   l b   i n . D E : T D E = 0

Forças da engrenagem:

F B = T B r B = 6302,5 3 = 2100,8   l b F C = T C r C = 4201,7   4 = 1050,4   l b

F D = T B r B = 2100,8 4 = 525,2   l b

Passo 4

Considere o esboço abaixo para determinarmos os momentos;)

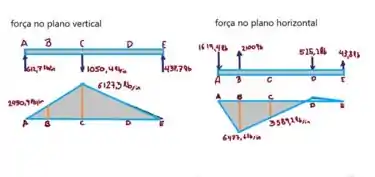
Em B + , M Y 2 + M Z 2 + T 2 = 2450,9 2 2 +   6477,6 2 2 +   6302,5 2 2 = 9364   l b / i n

Em C - , M Y 2 + M Z 2 + T 2 = 6127 , 3 2 +   3589 , 2 2 +   6302 , 52 2   =   9495   l b / i n

τ a l l = c J M Y 2 + M Z 2 + T 2 m a x J C = π 2 c 3 = M Y 2 + M Z 2 + T 2 τ a l l = 949 8 × 10 3 = 1,1868   i n 3

c = 0,911 i n . d = 2 c

d = 1,822   I N

Resposta

d = 1,822   I N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

48. A extremidade da viga em balanço está sujeita à carga mostrada. Determine as tensões principais na viga nos pontos A e B .
As cargas internas em uma seção da viga consistem em uma força axial de 500N , uma força de cisalhamento de 800N e duas componentes de momento 30N ⋅ m e 40N ⋅ m . Determine as tensões principais no po
As tensões principais em um ponto são mostradas na figura. Se o material for alumínio, para o qual E a l = 70G P a e v a l = 0,33 , determine as deformações principais.
As cargas internas que agem sobre uma seção transversal no eixo de acionamento de uma turbina de 150 mm de diâmetro consistem em uma força axial de 12,5 kN, um momento fletor de 1,2 kN.m e um momento
Um material está sujeiro às tensões principais σ x e σ y . Determine a orientação θ de um extensômetro coloca em um ponto, de modo que sua leitura da deformação normal responda apenas a σ y e não a σ