Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 78

O olhal está sujeito à força de 250 N. Determine as tensões de tração e compressão máxima na seção a-a. A seção transversal é circular e tem 6 mm de diâmetro. Use a fórmula da viga curva para calcular a tensão de flexão

Passo 1

Usando a fórmula da viga curva obtemos a linha neutra da seção a-a:

∫ A d A r   = 2 π r ` - r ` 2 - c 2 = 2 π 0,033 - 0,033 2 - 0,003 2 = 8,585756 × 10 - 4 m

Onde C é a distância do centróide da seção até a borda e r’ = C + R i n t e r n o

R = A ∫ A d A r = π × 0,003 2 8,585756 × 10 - 4 = 0,03293167 m

Passo 2

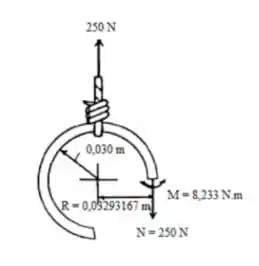
Obter os esforços na seção e fazer o diagrama de corpo livre:

Por somatório de forças: 250 - N = 0                     N = 250 N

Por somatório de momentos: M - 250 × 0,03293167 = 0                     M = 8,233 N . m

Passo 3

Obter as tensões, por carga axial e por flexão.

σ C = N A - M R - C o A C o r ' - R = 250 π × 0,003 2 - 8,233 × 0,03293167 - 0,036 π × 0,003 2 × 0,036 × 0,033 - 0,03293167 = - 354,4 M P a ( C )

σ T = N A + M R - C i A C i r ' - R = 250 π × 0,003 2 + 8,233 × 0,03293167 - 0,030 π × 0,003 2 × 0,030 × 0,033 - 0,03293167

σ T = 425,3 M P a ( T )

Resposta

σ C = - 354,4 M P a ( C )

σ T = 425,3 M P a ( T )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

P 1 e P 2 são aplicadas, como mostrado na figura, em direções perpendiculares ao eixo longitudinal de uma viga W310x60. Sabendo que P 1 = 25 k N e P 2 = 24 k N , determine as tenções principais e a te
(8.51) Três forças são aplicadas à componente de máquina ABD mostrado na figura. Sabendo que a seção transversal contendo o ponto H é um retângulo de 20mmx40mm, determine as tensões principais e a ten
Três placas de aço, cada uma com 13mm de espessura, são soldadas para formar uma viga em balanço. Para o carregamento mostrada, determine as tensões normal e de cisalhamento nos pontos a e b
Três placas de aço, cada uma com 13mm de espessura, são soldadas para formar uma viga em balanço. Para o carregamento mostrada, determine as tensões normal e de cisalhamento nos pontos a e b
8.57 Quatro forças são aplicadas a um perfil de aço laminado W8x28, conforme mostra a figura. Determine as tensões principais e a tensão de cisalhamento máxima no ponto a.