Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 72

O apoio tem seção transversal circular, cujo raio aumenta linearmente com a profundidade. Se for submetido à carga de compressão P, determine as tensões normais máxima e mínima que agem no material.

Passo 1

Muito parecida com a questão anterior, necessitamos descobrir em qual seção transversal estão as tensões máximas e mínimas no interior da estrutura.

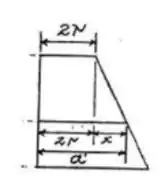
Sabemos que a força normal à seção será constante por toda a peça. N - P = 0           N = P

O momento em função de x será M a + x 2 - a 2 = 0                   M = 0,5 P x

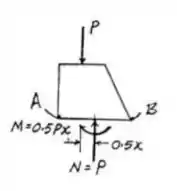
A área da seção transversal em função de x será A = π r + 0,5 x 2

E o momento de inércia I = π ( r + 0,5 x ) 4 4

Passo 2

Substituímos os valores obtidos acima nas equações de tensão normal de compressão

σ C = - N A - M × C I = - P π r + 0,5 x 2 - 0,5 P x × r + 0,5 x π r + 0,5 x 4 4 = - P π r + 2,5 x r + 0,5 x 3

Seu valor será máximo quando sua derivada for zero.

d d x - P π r + 2,5 x r + 0,5 x 3 = 0

Temos então X=0,4r

Substituindo esse valor em - P π r + 2,5 x r + 0,5 x 3 temos σ m á x = 0,368 P r 2 ( C )

Passo 3

Agora para a mínima (ou máxima de tração) faremos o mesmo, porém com o sinal da flexão oposto.

σ T = - N A + M × C I = - P π r + 0,5 x 2 + 0,5 P x × r + 0,5 x π r + 0,5 x 4 4 = P π - r + 1 , 5 x r + 0,5 x 3

Igualando : d d x P π - r + 1,5 x r + 0,5 x 3 = 0

Temos que x=2r

Substituindo em P π - r + 1,5 x r + 0,5 x 3 temos σ m i n = 0 , 0796 P r 2 ( T )

Resposta

σ m á x = 0,368 P r 2 ( C )

σ m i n = 0,0796 P r 2 ( T )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas forças são aplicadas a uma pequena coluna BD conforme mostrado. Sabendo que a porção vertical da coluna tem uma seção transversal de 1,5x2,4in., determine as tensões principais, os planos princip
(8.49)Duas forças são aplicadas a uma pequena coluna BD conforme mostrado. Sabendo que a porção vertical da coluna tem uma seção transversal de 1,5x2,4in., determine as tensões principais, os planos p
8,47:(Três forças são aplicadas à barra mostrada na figura. Determine as tensões normal e de cisalhamento (a) no ponto a, (b) no ponto b e (c) no ponto c.) Resolva o problema 8.47 considerando que for
Três forças são aplicadas à barra mostrada na figura. Determine as tensões normal e de cisalhamento (a) no ponto a, (b) no ponto b e (c) no ponto c.
Três forças são aplicadas à componente de máquina ABD mostrado na figura. Sabendo que a seção transversal contendo o ponto H é um retângulo de 20mmx40mm, determine as tensões principais e a tensão de