Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 94
94- Duas correias de transmissão passam por duas roldanas soldadas a um eixo apoiado por mancais em e . A roldana em tem um raio de , e a roldana em tem um raio de . Sabendo que o sistema roda a uma velocidade constante, determine a tração , as reações em e . Considere que o mancal em não exerce qualquer esforço axial e despreze os pesos das roldanas e do eixo.
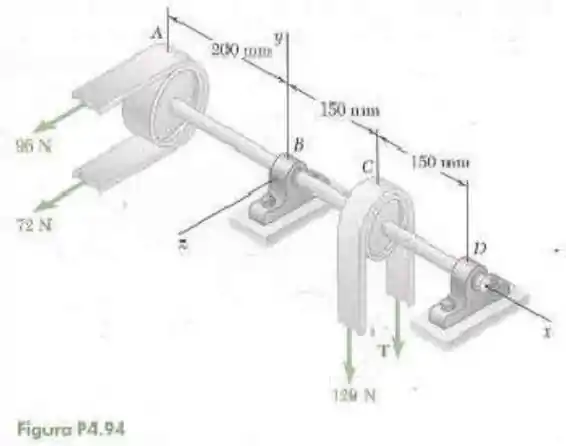
Passo 1
Como não existe (pelo enunciado ) e como não há nenhuma força atuando em logo também não existirá então o sistema de forças nesse sistema será:
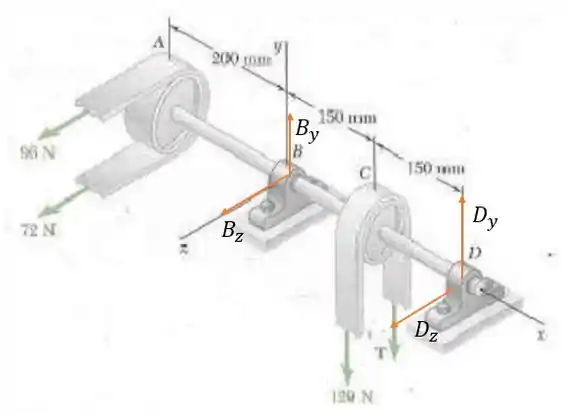
Onde o raio da polia em é de e o raio da polia em é de
Passo 2
Vamos fazer a somatória dos momentos em até por que ela está na origem e para isso nós devemos tomar cuidado com as distâncias relativas de todas as forças em relação a esse ponto.
Começando com a força de nós temos uma força relativa de:
Agora a distância relativa para a força de :
A distância relativa para a força de :
E a distância relativa para a força :
Além da distância relativa para :
Passo 3
Isso nos dá uma somatória dos momentos em igual :
Fazendo todas essas determinantes nós temos:
Somando todas as componentes que tem nós temos:
O que nos responde a letra .
Agora para as componentes que tem .
E somando as que tem :
O que nos dá uma reação em de forma vetorial igual a:
Passo 4
Agora fazendo a somatória de todas as forças nós teremos a reação em :
Somando as componentes que tem nós temos:
E as componentes que tem :
O que nos dá uma reação vetorial em igual a: