Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 97
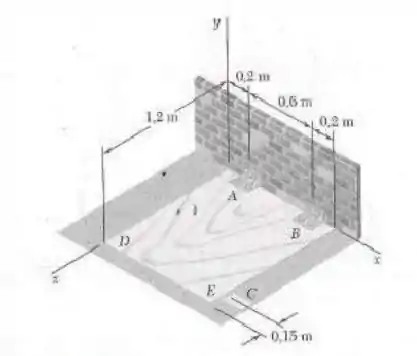
4.97. Uma abertura no piso é coberta por uma folha de madeira compensada de , com massa de 18 kg. A folha é articulada em A e B e é mantida em uma posição ligeiramente acima do solo por um pequeno bloco C. Determine o componente vertical da reação (a) em A, (b) em B, (c) em C.
Passo 1
Vamos começar fazendo um desenho com os pontos importantes da imagem
Esse G é o centro de gravidade da folha d e madeira, onde age a força peso, falando nela, vamos calcular
Passo 2
Bom, sabemos que a folha de madeira está parada, então
Vamos então somar todos os componentes que compões a o momento em A
As forças que agem são a força peso, a força de reação em A, B e C, então
Vamos descobrir quem são esses vetores
Então
Vamos lembrar que para produto vetorial
Então
Então
E
Passo 3
Agora de 1, nós tiramos
Agora vamos calcular 2
Agora só falta calcular a força de reação em A, para isso podemos usar
Pronto. Agora temos todas as forças de reação.
Resposta
(a)
(b)
(c)