Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 105
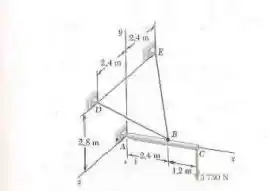
4.105. Sobre uma lança de 3 m atua uma força de como mostrado na figura. Determine a tração em cada cabo e a reação em A.
Passo 1
Vamos fazer um desenho com os pontos importantes da imagem
Bem, o que precisamos fazer é igualar o momento à 0, já que o sistema está parado, e para isso a gente vai precisar dos vetores posição, vamos calcular então
Vamos aproveitar e calcular o módulo, a gente já já vai precisar
E agora o outro cabo
Agora o módulo, mas repare que são os mesmos números que em módulo, então o módulo do vetor é o mesmo
E agora podemos determinar as rações nos cabos, porque podemos determinar os vetores unitários que apontam na direção da tração
E
Passo 2
Agora a gente pode usar o esquema do momento
Então
A gente não pode esquecer a força peso, jamais.
Agora a gente tem tudo
Lembrando
E igualando os componentes à 0 temos
E
Passo 3
De (1) nós tiramos
A gente pode cortar
Agora a gente substitui isso na equação (2)
Então
Passo 4
Agora a gente pode determinar a força de reação em A usando o somatório das forças em A.
Vamos começar em x
Então
Agora em y
E por fim em z
Então