Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 125
125- A estrutura é sustentada por uma rótula em e por três cabos. Para , determine a tração em cada cabo e a reação em .
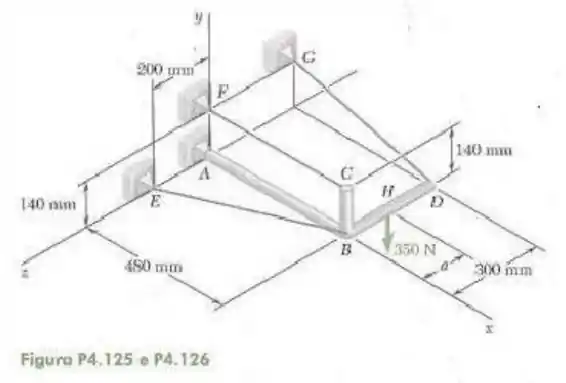
Passo 1
Não confunda o desenho temos apenas os cabos , e . E a rótula exerce apenas reações nos três eixos (que consideraremos como positivas).
A vetorização das forças nesses cabos serão iguais a:
Passo 2
Agora vamos calcular o momento em e pra isso precisamos das distâncias relativas a e .
Isso nos dá uma somatória de momentos em igual a:
Fazendo todas essas determinantes nós temos:
Se fizermos a soma de todas as componentes que contém nós teremos:
Agora a soma de todos os componentes que tem :
E todos os que tem :
Passo 3
Agora vamos fazer a somatória das forças nos três sentidos para encontrar as reações em .
Fazendo a soma nos três sentidos nós temos:
Dessa forma a reação em de forma vetorial é: