Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 210
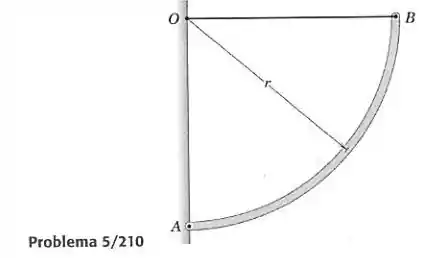
A barra uniforme de massa está curvada em um quarto de arco circular, no plano vertical, e bascula livremente em . A barra é mantida em posição pelo arame horizontal de até . Determine o módulo da força sobre o pino em .
Passo 1
Temos atuando na barra a tração do arame, as reações em e o peso do arco. Para achar as forças em , devemos determinar em qual ponto será aplicada a força peso. Esse ponto é o centroide do arco, que tem distância até o centro conhecida e dada na figura:
Passo 2
Fazendo a soma das forças em para o arco ser zero, temos:
Agora fazendo o momento em relação a :
Dividindo os dois lados por :
Passo 3
Agora basta calcular o módulo:
Resposta
Exercícios de Livros Relacionados
Calcule a distância h - medida desde a base até o centroide do volume do cone circular truncado.
A figura representa uma peça plana de uma chapa metálica, simétrica em relação ao eixo A-A e que tem o contorno superior parabólico. Escolha as suas próprias coordenadas e calcule a distância h - a pa
Determine a coordenada y do centroide da área sombreada mostrada. (Observe os cuidados citados no Prob. 5/28).
Determine a coordenada x do centroide do segmento esférico sólido.
Determine a coordenada z do centroide do volume gerado pela revolução de 180° da área sombreada em torno do eixo z - .