Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 65
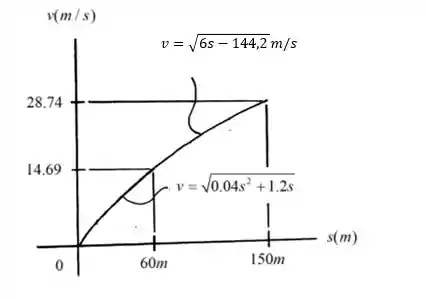
A aceleração de uma lancha de corrida partindo do repouso é descrita pelo gráfico. Construa o gráfico .
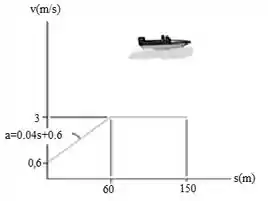
Passo 1
Sabemos que, quando o gráfico é conhecido, podemos calcular a aceleração em qualquer posição . Utilizaremos a Eq.(1).
(1)
Passo 2
Devemos analisar o comportamento da velocidade em dois intervalos (0:60) e (60:150), então:
Para , a condição inicial é .
Para ,
Para condição inicial é
Para ,
Resposta
O gráfico está mostrado abaixo.
Exercícios de Livros Relacionados
O piloto de um avião de transporte a jato leva os motores a plena potência de decolagem antes de liberar os freios enquanto a aeronave está parada sobre a pista. O empuxo do jato permanece constante,
Um avião a jato com uma velocidade de pouso de 200k m / h tem um máximo de 600m de pista disponível após tocar o solo no qual deve reduzir sua velocidade para 30k m / h . Calcule a aceleração média a
Nos estágios finais de um pouso na Lua, o módulo lunar desce sob retropropulsão de seu motor de descida até h = 5m da superfície lunar onde tem uma velocidade para baixo de 2m / s . Se o motor de desc
O carro está viajando com uma velocidade constante v 0 = 100k m / h na parte horizontal da estrada. Quando o plano inclinado a 6 %( tan θ = 6 / 100 ) é encontrado, o condutor não altera a posição do
Uma menina rola uma bola para cima em um plano inclinado e deixa esta retornar para ela. Para o ângulo θ e a bola em questão, a aceleração da bola ao longo da inclinação é constante em 0,25 g , dirigi