Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 25
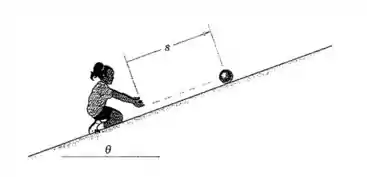
Uma menina rola uma bola para cima em um plano inclinado e deixa esta retornar para ela. Para o ângulo e a bola em questão, a aceleração da bola ao longo da inclinação é constante em , dirigida para baixo no plano inclinado. Se a bola é liberada com uma velocidade de , determine a distância em que esta se move para cima no plano inclinado antes de inverter o seu sentido e o tempo total é necessário para a bola retornar à mão da criança.
Passo 1
A questão pode parecer meio complicada, mas na verdade você pode resolver exatamente como se estivesse no plano: a única diferença é o valor da aceleração!
Vamos dizer que o é a mão da menina, então o sentido positivo é ladeira acima.
Nosso primeiro objeito é encontrar a distância que a bola percorre no plano inclinado:
Sabemos que, no topo da trajetória, a velocidade da bola se anula:
Passo 2
E agora para descobrir o tempo necessário para o movimento vamos começar analisando a subida:
E sabemos que a descida vai levar exatamente o mesmo tempo, então o intervalo total é:
Resposta
A distância percorrida é e o tempo total é .