Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 57
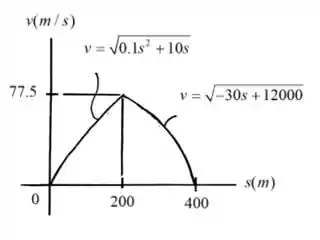
O carro de corrida tipo Dragster parte do repouso e move-se ao longo de uma pista reta com uma aceleração – desaceleração descrita pelo gráfico. Construa o gráfico v-s para , e determine a distância percorrida antes de o dragster entrar em repouso novamente.
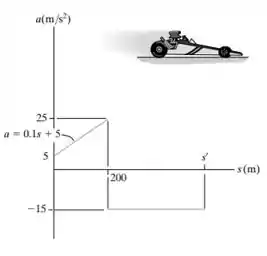
Passo 1
Para a construção do gráfico, devemos calcular a velocidade em dois intervalos distintos.
Para , então:
Para
Para
Passo 2
Sabe-se que quando , , então:
Resposta
O gráfico está mostrado abaixo.
Exercícios de Livros Relacionados
A aceleração de uma partícula é dada por a = - k s 2 , onde a é em metros por segundo ao quadrado, k é uma constante, e s é em metros. Determine a velocidade da partícula como uma função de sua posiçã
Dados experimentais para o movimento de uma partícula ao longo de uma linha reta forneceram medidas dos valores da velocidade v para várias coordenadas de posição s . Uma curva suave é desenhada passa
A posição de uma partícula é dada por s = 2 t 3 - 40 t 2 + 200 t - 50 , onde s é em metros e t é em segundos. Represente graficamente a posição, velocidade e aceleração como funções do tempo para os p
O deslocamento de uma partícula que se move ao longo do eixo s é dado por s = - 2 + 3 t e - 0,5 t , onde s é em metros e t é em segundos. Represente graficamente o deslocamento, a velocidade e a acele
A aceleração de uma partícula que está se movendo ao longo de uma linha reta a = - k v , onde a é em metros por segundo ao qudrado, k é uma constante, e v é a velocidade em metros por segundo. Determi