Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 29
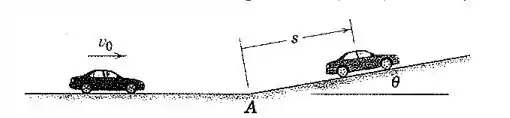
O carro está viajando com uma velocidade constante na parte horizontal da estrada. Quando o plano inclinado a é encontrado, o condutor não altera a posição do pedal do acelerador e consequentemente o carro desacelera a uma taxa constante . Determine a velocidade do carro (a) segundos após passar pelo ponto e (b) quando .
Passo 1
Vamos começar procurando a velocidade do carro segundos após passar pelo ponto .
Já temos a veloicdade inicial e a aceleração é , vamos substitutir esses valores na equação horária da velocidade:
Pelo enunciado é o ângulo que tem como tangente. Para ângulos muito pequenos (como é o caso desse), sabemos que vale a seguinte aproximação:
Então:
Passo 2
Agora queremos calcular a velocidade depois que o carro percorre m. Como não estamos fazendo nenhuma menção ao tempo, é uma boa ideia usar essa equação aqui:
Resolvido!
Resposta
(a)
(b)