Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 38
O pequeno bloco tem espessura de 5 mm. Se a distância de tensão no apoio desenvolvida pela carga variar como mostra a figura, determine a força F aplicada ao bloco e a distância d até o ponto onde ela é aplicada.
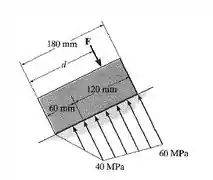
Passo 1
Bom, a chave dessa questão é entender o comportamento das tensões, pois a área da distribuição das tensões é igual a força aplicada no centro desta área.
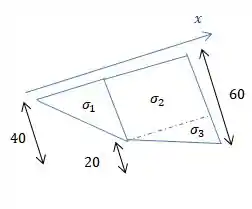
Para facilitar, vamos separar as tensões em um triângulo (que representa a força ), em um retângulo (força ) e em outro triângulo (força ). Dividimos nessas áreas, pois conhecemos bem o centro dessas áreas para saber aonde essas 3 forças serão aplicadas.
Tendo a nossa tensão dada para a força e a área :
Essa área é a área do corpo aonde está ocorrendo essa tensão, para isso, precisamos olhar para as dimensões do corpo, aqui a largura será e a profundidade será .
Da onde encontramos a nossa força:
Fazemos o mesmo para a força :
E a nossa força , será:
E finalmente para a força ...
Passo 2
Como o corpo está em equilíbrio, a força F deve ser o somatório de , e.
Passo 3
Para acharmos a distância d, precisamos utilizar a segunda equação de equilíbrio, que é a do momento.
Mas para isso, precisamos saber aonde são aplicadas as nossas forças , e .
Sabemos que será aplicada no centro do retângulo, e que e serão aplicadas há uma distância de 2/3 da ponta do triângulo, ficando assim:
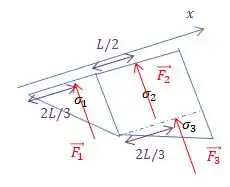
Conhecendo nossas dimensões, podemos encontrar a distância de cada força até a extremidade esquerda da peça:
Agora, a gente pode prosseguir:
Vamos calcular que o momento na extremidade esquerda deve ser nulo.
Tomando o sentido anti-horário como positivo, teremos:
Substituindo o que temos:
E, portanto, para que essa peça esteja em equilíbrio, a força é de e deve ser aplicada a da extremidade esquerda.
E aí, matamos mais uma, bora pra próxima?