Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 113

Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.

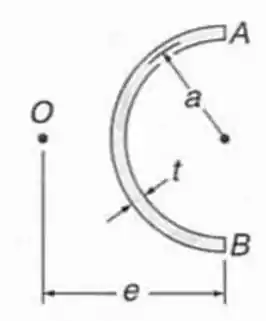
Passo 1

Para acharmos a localização do ponto O , ou seja, a distância e vamos fazer o seguinte passo a passo:

  1. Determinar o momento de inércia I .
  2. Achar a tensão cisalhante.
  3. Calcular, por meio de integral, o momento aplicado.

Passo 2

Aqui vamos determinar o momento de inércia de meia circunferência de parede fina. Mas antes vamos lembrar da circunferência completa de parede fina. de raio r e espessura t :

I c i r c u l o = π r 3 ⋅ t

Para meio círculo, ou circunferência, é só dividir por 2. Vamos também substituir o raio r = a

I = 1 2 π a 3 ⋅ t

Passo 3

Para achar a tensão cisalhante vamos primeiro achar o momento estático da parte A B até um dado ponto x :

Q A B = A y -

Como estamos falando de um círculo é válido utilizar as coordenadas polares, então vamos ter:

A = a ⋅ θ ⋅ t

Agora a gente tem que lembrar, ou olhar na tabelinha do final do livro rs, que a posição do centroide de um arco de circunferência é igual a:

x - = r ⋅ s e n ( α ) α

Onde α é a metade do ângulo interno ( θ ). Mas a gente precisa achar y - então:

y - = x - ⋅ c o s ⁡ ( α )

Sendo assim,

y - = r ⋅ s e n α α ⋅ c o s ⁡ ( α )

y - = a ⋅ s e n ( α ) α ⋅ c o s ⁡ ( α )

Achando o momento estático:

Q = a ⋅ θ ⋅ t ⋅ a ⋅ s e n ( α ) α ⋅ c o s ⁡ ( α )

Q = a 2 ⋅ t ⋅ θ α ⋅ s e n 2 α 2

Q = a 2 ⋅ t ⋅ s e n θ

Agora é só substituir na equação da tensão cisalhante:

τ = V Q I t

τ = V a 2 ⋅ t ⋅ s e n θ I t

τ = V a 2 ⋅ s e n θ I

Passo 4

Para achar o momento M a gente vai ter que integrar a tensão cisalhante pela área da seguinte forma:

M = ∫ a ⋅ τ ⋅ d A

Substituindo τ

M = ∫ a ⋅ V a 2 ⋅ s e n θ I ⋅ d A

Transformando d A em t a ⋅ d θ

M = ∫ V a 3 ⋅ s e n θ I ⋅ t a ⋅ d θ

M = V a 3 ⋅ a t I ∫ s e n θ ⋅ d θ

M = V a 4 t I ⋅ - cos ⁡ θ 0 π

M = V a 4 t I ⋅ 2

Substituindo I

M = V a 4 t 1 2 π a 3 ⋅ t ⋅ 2

M = V a 1 2 π ⋅ 2

M = 4 V a π

Como esse momento é igual ao momento aplicado em O pela cortante, vamos ter:

M = M V

4 V a π = V ⋅ e

e = 4 a π

Resposta

e = 4 a π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é feita de um material cerâmico cuja tensão de flexão admissível é σ a d m = 5 MPa e tensão de cisalhamento τ a d m = 2,8 MPa. Determine a largura b da viga, se a altura for h=2b.
A viga T de aço em balanço foi montada com duas chapas soldadas como mostra a figura. Determine as cargas máximas P que podem ser suportadas com segurança pela viga, se a tensão de flexão admissível f
A viga é construída com duas tábuas presas uma à outra na parte superior e na parte inferior por duas fileiras de pregos espaçados de 150 mm. Se cada prego puder suportar uma força de cisalhamento de
A viga é construída com duas tábuas presas uma à outra na parte superior e na parte inferior por duas fileiras de pregos espaçados de 150 mm. Se uma força de cisalhamento interna V = 3 k N for aplicad
Determine a força de cisalhamento máxima V que a escora pode suportar se a tensão de cisalhamento admissível para o material for τ a d m = 40M P a