Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 128b

Para a viga em balanço e o carregamento dado, determinar o ponto onde a tensão de cisalhamento é mázima e o corresponde valor da tensão: (b) ao longo da linha D ' E ' de uma perna.

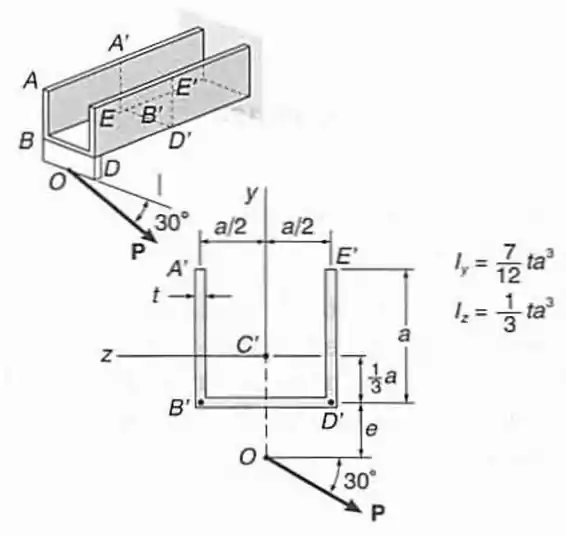
Passo 1

Vamos calcular o momento estático para cada uma das opções E ' D ' :

Q = A ⋅ y -

A = t ⋅ ( a - y )

y - = a + 3 y 6

Q = t ⋅ a - y ⋅ a + 3 y 6

Q = t 6 ⋅ ( a 2 + 3 a y - a y - 3 y 2 )

Q = t 6 ⋅ ( a 2 + 2 a y - 3 y 2 )

Passo 2

Agora vamos substituir na equação da tensão cisalhante, primeiro para E ' D ' :

τ = V Q I t

τ = V I t ⋅ t 6 ⋅ ( a 2 + 2 a y - 3 y 2 )

τ = V 6 I ⋅ ( a 2 + 2 a y - 3 y 2 )

Para acharmos o valor mázimo basta derivar e igualar a zero:

d τ d y = 0

V 6 I 2 a - 6 y = 0

Logo o ponto onde a tensão cisalhante é mázima é em y = a 3

Passo 3

Agora vamos substituir a força cortante, o momento de inércia e o ponto de tensão cisalhante máxima na equação:

τ = V Q I t

Para E ' D '

τ = P ⋅ cos ⁡ 30 1 3 t a ³ t ⋅ t 6 ⋅ ( a 2 + 2 a y - 3 y 2 )

τ = P ⋅ cos ⁡ 30 1 3 t a ³ t ⋅ t 6 ⋅ a 2 + 2 a ⋅ a 2 - 3 a 2 2  

τ = P ⋅ cos ⁡ 30 2 t a ³ ⋅ a 2 + 2 a ⋅ a 2 - 3 a 2 2  

τ = P ⋅ cos ⁡ 30 2 t a ³ ⋅ a 2 + a ² - 3 a 2 4  

τ = P ⋅ cos ⁡ 30 2 t a ³ ⋅ 5 a 2 4  

τ = P ⋅ cos ⁡ 30 2 t a ⋅ 5 4  

τ = 0,541 P t a  

Resposta

Ponto y = a / 3

Vale:

τ = 0,541 P t a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga consiste em cinco pranchas com seção transversal de 1,5 x 6 in. Conectadas por parafusos de aço espaçados longitudinalmente de 9 in. Sabendo que a força cortante na viga é vertical e igual a
A seção transversal de uma viga extrudada é um quadrado vazado de lado a = 3i n . e espessura t = 0,25 . Para uma força cortante vertical de 15k i p s ,determine a tensão de cisalhamento máxima na vig
Para uma viga feita de dois ou mais materiais diferentes módulos de elasticidade. Mostre que a Equação (6.6) τ m e d = V Q I t permanece válida desde que Q e I sejam calculados usando a seção transfor
Uma placa de 6,35 mm de espessura é enrugada, conforme mostra a figura, e depois usada como uma viga . Para uma força cortante vertical de 5,34 kN, determine (a) a tensão de cisalhamento no ponto B. E
Uma viga extrudada tem a seção transversal mostrada na figura é uma parede de espessura uniforme de 3 ymm. Para força cortante vertical de 10 kN, determine (a) o tensão de cisalhamento no ponto A, (b)