Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 116

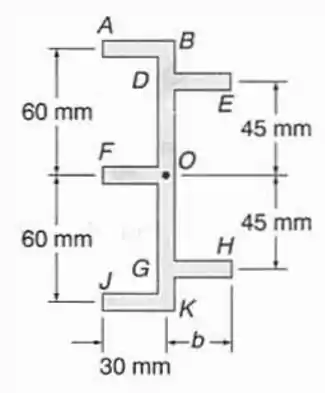
Uma viga de parede fina com espessura uniforme tem a seção transversal mostrada. Determinar a dimensão b , para que o centro de cisalhamento da viga esteja localizado no ponto indicado.

Passo 1

Para acharmos a localização do ponto O , ou seja, a distância e vamos fazer o seguinte passo a passo:

  1. Achar a tensão cisalhante.
  2. Calcular, por meio de integral, a força interna atuante na bara.
  3. Com essa força achar o momento atuante.

Passo 2

Vamos dividir esta seção em 3 partes: A B   e   D E . Para a parte A B vamos achar a tensão por meio do momento estático:

Q = A ⋅ y -

Q A B = t x ⋅ 60

Substituindo na tensão:

τ = V Q I t

τ = V I x ⋅ 60

Agora fazemos a integral para achar a força

F = ∫ τ ⋅ d A

F = ∫ V I x ⋅ 60 ⋅ d A

Substituindo d A = t ⋅ d x

F = ∫ V I x ⋅ 60 ⋅ t ⋅ d x

F = V I ⋅ 60 ⋅ t ∫ x ⋅ d x

F = V I ⋅ 60 ⋅ t ⋅ x 2 2 0 30

F = V I ⋅ 60 ⋅ t ⋅ 30 2 2

F A B = V I ⋅ t ⋅ 27000

Passo 3

A mesma coisa para D E

Q = A ⋅ y -

Q D E = t x ⋅ 45

Substituindo na tensão:

τ = V Q I t

τ = V I ⋅ x ⋅ 45

Agora fazemos a integral para achar a força

F = ∫ τ ⋅ d A

F = ∫ V I ⋅ x ⋅ 45 ⋅ d A

Substituindo d A = t ⋅ d x

F = ∫ V I ⋅ x ⋅ 45 ⋅ t ⋅ d x

F = V I ⋅ 45 ⋅ t ∫ x ⋅ d x

F = V I ⋅ 45 ⋅ t ⋅ x 2 2 0 b

F D E = V I ⋅ 45 ⋅ t ⋅ b 2 2

Passo 4

Agora vamos igualar os momentos gerados pelas duas forças, mas repare que fizemos apenas para a parte superior então na verdade as forças formam pares binários com suas respectivas.

M 1 = M 2

Onde M 1 representa o binário A B   e   J K

M 1 = F A B ⋅ 120

M 1 = V I ⋅ t ⋅ 27000 ⋅ 120

E M 2 representa o binário D E   e   H G

M 2 = F D E ⋅ 90

M 2 = V I ⋅ 45 ⋅ t ⋅ b 2 2 ⋅ 90

Igualando os dois:

V I ⋅ t ⋅ 27000 ⋅ 120 = V I ⋅ 45 ⋅ t ⋅ b 2 2 ⋅ 90

27000 ⋅ 120 = 45 ⋅ b 2 2 ⋅ 90

b 2 = 1600

b = 40   m m

Resposta

b = 40   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250m m e o cisalhamento apl
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine o espaçamento máximo s para os parafusos se cada um deles puder resistir a um cisalhamento de20k N e o cisalhamento apl
A viga está sujeita a um cisalhamento V = 800N . Determine a tensão de cisalhamento média desenvolvida nos pregos ao longo dos lados A e B se eles estiverem espaçados de s = 100 m m . Cada prego tem d
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150m m e espessura de 12m m . Se os parafusos estiverem espaçados de s = 200 m m , determine a força de c
A viga-mestra de alma dupla é composta por duas chapas de compensado presas a elementos de madeira na parte superior e na parte inferior. Se cada elemento de fixação puder suportar 3k N em cisalhament