Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 93

O alçapão uniforme de por pesa e é mantido aberto pelo suporte leve no ângulo . Calcule a compressão na biela e a força suportada pela dobradiça normal ao eixo da dobradiça. Suponha que as dobradiças atuam nas extremidades da borda inferior.

Passo 1

Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar a força de compressão na biela em e a força suportada pela dobradiça normal ao seu eixo, devido ao peso da placa uniforme de . Vamos começar desenhando o diagrama de corpo livre do nosso problema.

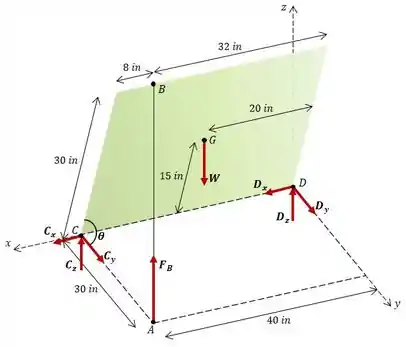
Onde:

Podemos descrever vetorialmente o peso da porta como:

O mesmo para a tensão utilizando seu vetor unitário na direção . As coordenadas dos pontos e são:

E, finalmente, a tensão no cabo pode ser definida vetorialmente como:

Passo 2

Uma vez que o corpo está em equilíbrio, podemos fazer o somatório dos momentos de cada uma das forças que agem na porta em torno do ponto , por exemplo, e ele deve ser nulo.

Para isso, precisamos dos vetores direção dos pontos de aplicação das forças até o ponto :

Para facilitar nossos cálculos, vãos resolver separadamente o momento causado por cada uma das forças. Começando pela tensão no cabo:

Agora para o peso:

E para o as reações da dobradiça :

Passo 3

Tá, mas e agora?

Até aqui temos que:

Para satisfazer a condição de equilíbrio, as componentes , e separadamente também devem ser nulas. Então:

O que nos da um sistema de três equações e três incógnitas. Pela primeira equação temos:

Substituindo na segunda e terceira equação:

Passo 4

Mas calma que ainda não acabou! Hehe

Lembra que o que nos foi pedido foi a reação normal na dobradiça , não na dobradiça . Essa reação pode ser facilmente obtida pelo equilíbrio de forças nas direções e , já que temos todas as demais forças do sistema. Sendo assim:

Mas você deve estar se perguntando: “por que não consideramos a reação da dobradiça?”. Desconsideramos pois foi pedida a reação normal na dobradiça , que está localizada no eixo , ou seja, a reação perpendicular a esse eixo. Finalmente temos que: