Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 76

O suporte grande é construído em chapa pesada que possui massa ρ por unidade de área. Determine as reações de força e momento no parafuso de suporte em O .

Passo 1

Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar as reações de forças e momentos no parafuso de suporte em O devido ao peso da chapa. Vamos começar desenhando o diagrama de corpo livre do nosso problema.

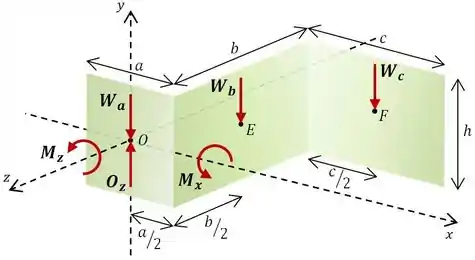
Observe que, por se tratar de um engaste, deveríamos ter representado três reações de força e três reações de momento no ponto O . Entretanto, todas as forças aplicadas são paralelas ao eixo y , o que indica que teremos reação de força apenas nessa direção e que não haverá momento neste sentido, restando apenas O y , M x e M z .

Além disso, vamos dividir o corpo em três peças ( a , b e c ) com seus respectivos pesos atuando no centro de massa de cada uma, cujas coordenadas são:

O = 0,0 , 0

E = a 2 , 0 , - b 2

F = a 2 + c 2 , 0 , - b

E os pesos:

W a = a h ρ g

W b = b h ρ g

W c = c h ρ g

Passo 2

Então bora começar nossos cálculos! Esse problema pode ser facilmente resolvido utilizando as equações de equilíbrio de forças na direção z e de momento nas direções x e y , é exatamente isso que vamos fazer!

∑ F y = 0

O y - W a - W b - W c = 0

O y = a h ρ g + b h ρ g + c h ρ g

O y = h ρ g a + b + c

Passo 3

Para os momentos em torno de O , basta multiplicarmos os pesos pelas suas distâncias até este ponto, dadas pelas coordenadas dos pontos O , E e F de aplicação.

∑ M x = 0

M x - W b b 2 - W c b = 0

M x = b h ρ g b 2 + c h ρ g b = 0

M x = b h ρ g b 2 + c

∑ M z = 0

M z - W b a 2 - W c a 2 + c 2 = 0

M z = b h ρ g a 2 + c h ρ g a 2 + c 2

M z = h ρ g 2 ( a b + a c + c 2 )

Até que não foi tão difícil né? Partiu pra próxima!

HYPERLINK "https://emojiterra.com/pt/rosto-piscando/"

Resposta

O x = 0

O y = h ρ g a + b + c

O z = 0

M x = b h ρ g b 2 + c

M y = 0

M z = h ρ g 2 ( a b + a c + c 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as forças em cada cabo necessárias para suportar uma carga com 250 kg de massa.
Determine as intensidades de F 1 ,F 2eF 3 para o equilíbrio da partícula.
5.63. A haste uniforme lisa AB é apoiada por uma junta esférica em A, a parede em B e o cabo BC. Determine as componentes da reação em A, a tensão no cabo e a reação normal em B, se a barra possui mas
A laje de concreto uniforme tem massa de 2400k g . Determine a tração em cada um dos três cabos de apoio paralelos quando a laje é mantida no plano horizontal, conforme mostrado na figura.
O carrinho sustenta o engradado uniforme com massa de 85k g . Determine as reações verticais sobre os três rodízios em A ,B e C . O rodízio em B não aparece na figura. Despreze a massa do carrinho.