Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 26
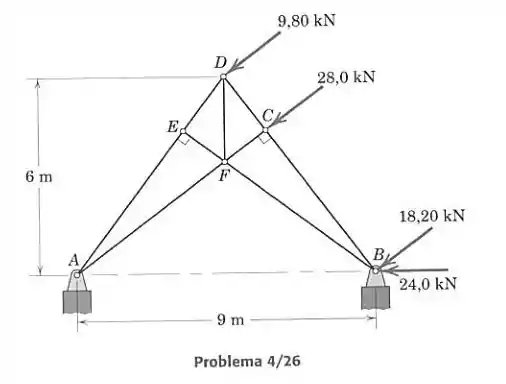
A análise do vento atuando em uma pequena igreja do Havaí, que suportou os ventos de 280 km/h do furacão Iniki em 1992, mostrou que as forças transmitidas para cada um dos painéis de treliça do telhado foram como indicado. Trate a estrutura como uma treliça simples simétrica e despreze qualquer componente horizontal da reação do apoio em . Identifique o elemento da treliça que suporta a maior força, em tração ou compressão, e calcule esta força.
Passo 1
Vamos calcular as equações de equilíbrio para as forças externas e as equações para cada nó da treliça. Primeiro, precisamos analisar os ângulos de inclinação das barras. Na figura vemos os ângulos que devemos conhecer.
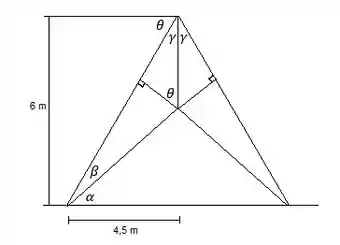
Podemos encontrar o tamanho do lado por Pitágoras:
Então:
Além disso, observamos facilmente que . Temos também pela soma dos ângulos internos do triangulo:
E finalmente:
Passo 2
Agora vamos às equações de equilíbrio da treliça como um todo. O tamanho do lado é calculado da seguinte maneira:
Passo 3
Agora iremos calcular as equações de equilíbrio para os nós. Teremos T indicando que a força é de tração e C que é de compressão. Nas equações colocaremos sempre a direção da força de um elemento como se fosse de tração, e se o valor for negativo ela será na verdade de compressão.
Nó A:
pode ser considerada como uma única barra retilínea, então devemos ter obrigatoriamente para o equilíbrio:
Passo 4
Nó D:
Passo 5
Nó F:
Podemos ver facilmente olhando para C que
Então a maior força é em :