Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 45

O anel D de 35kg é abandonado do repouso na posição mostrada e é parando por uma placa conectada na extremidade em C da haste vertical ABC. Sabendo que E=200 GPa para ambas as porções da haste, determine a distância h para que a máxima tensão na haste seja de 250 MPa.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

Porção BC tem seção transversal menor, portanto

P m = σ a l l A B C = 250 M P a π 4 0,030 m 2 = 176,7   k N  

Energia máxima de tensão (para P m = 176,7   k N )

U m = ∑ P m 2 L i 2 A i E = P m 2 2 E ∑ L i A i = ( 176,7   k N   ) ² 2 ( 200   G P a )   2 m π 4 ( 0,040 m ) ² + 1,5 m π 4 ( 0,030 m ) ²

U m = 78,06 × 1 0 - 3 1591,6 + 2122,1 = 289,9   J

Máx. deflexão:

1 2   P m △ m = U m

1 2 176,7   k N △ m = 289,9 J

△ m = 3,28 × 1 0 - 3 m = 3,28 m m

Trabalho de peso = 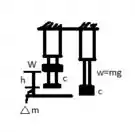U m

W h + △ m = U m

( m g ) h + △ m = U m

( 35   k g ) ( 9.81 m / s ² )   h + △ m = 289,9 J

h + △ m = 0,8443 m = 844,3 m m

h = 844,3 - △ m = 844,3 - 3,28 = 841 m m

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de h = 841 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o módulo de resiliência para cada um dos seguintes tipos de ligas de alumínio:
A barra B C é feita de um aço para o qual a tensão de escoamento é 300M P a e o módulo de elasticidade é de 200G P a . Sabendo que a energia de deformação de 10J deve ser adquirida pela barra quando l
Determine o módulo de resiliência para cada um dos seguintes tipos de liga metálica:
Um pino de aço de 6m m de diâmetro em B é usado para conectar a tira de aço D E e duas tiras de alumínio, cada uma com 20m m de largura por 5m m de espessura. O módulo de elasticidade é de 200G P a pa
Usando E = 200G P a , determine (a) a energia de deformação da barra de aço A B C quando P = 25k N e (b) a densidade de energia de deformação correspondente nas partes A B e B C da barra.