Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 2
Determine o módulo de resiliência para cada um dos seguintes tipos de ligas de alumínio:
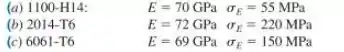
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Esta questão é basicamente aplicação de fórmula. Sabemos que o módulo de resiliência de um material é dado por:
Onde é a tensão de escoamento e é o módulo de elasticidade;
Passo 2
Agora, basta substituir os dados fornecidos. Para a letra teremos:
Passo 3
Fazendo o mesmo para a letra
Passo 4
Por fim, para a letra c:
Prontinho, questão feita! Até a próxima.
Resposta
Exercícios de Livros Relacionados
Uma força axial e cenrada, de intensidade P = 40k N , é aplicada à barra de aço mostrada. Determinar o máximo valor da tensão normal. (a) em A; (b) em B
Uma força axial é centrada, de intensidade P = 270k N é aplicada à barra de aço mostrada. Determine o máximo valor da tensão normal na barra, sabendo-se que: d = 120m m e r = 15m m d = 100m m e r = 25
Uma força axial e cenrada, de intensidade P = 40k N , é aplicada à barra de aço mostrada. Determinar o máximo valor da tensão normal. (a) em A; (b) em B
A tensão normal admissível para o aço da barra mostrada vale 125 Mpa. Determinar a máxima força P admissível, axial e centrada, que pode ser aplicada a barra sabendo-se que d = 100 m m r = 15m m r = 2
Uma força axial é centrada, de intensidade P = 270k N é aplicada à barra de aço mostrada. Determine o máximo valor da tensão normal na barra, sabendo-se que: d = 120m m e r = 15m m d = 100m m e r = 25