Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 10
Usando determine (a) a energia de deformação da barra de aço quando e (b) a densidade de energia de deformação correspondente nas partes e da barra.
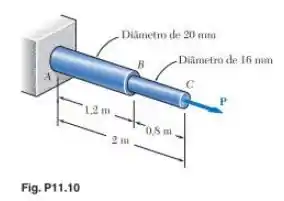
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Vamos, primeiramente, listar a área das barras:
Como teremos que a energia de deformação será:
Como os valores são fornecidos, basta substituir os valores de cada parcela da barra. Fazendo isso:
Passo 2
Agora, para achar a densidade de energia de deformação, precisamos primeiro da tensão em cada barra, sabemos que:
Substituindo:
Com a tensão, podemos obter a densidade de energia de deformação, através da seguinte fórmula:
Substituindo:
Resposta
Exercícios de Livros Relacionados
A temperatura da barra composta do P r o b .2.43 é aumentada para 80 ° C . Sabendo-se que, para o aço E = 200G P aeα = 11,7.10 - 6° C - 1 , para o latão E = 105G P aeα = 20,9.10 - 6° C - 1 , e que nen
Uma barra de alumínio ( E = 70G P a ;α = 23,6.10 - 6° C - 1 ) e uma haste de aço ( E = 200G P a ;α = 11,7.10 - 6° C - 1 ) tem as dimensões mostradas, a uma temperatura de 20°C. A haste de aço é aqueci
Em um teste de tração, uma barra de 20 m m de diâmetro, feita de um plástico que acaba de ser desenvolvido, é submetida a uma força P de intensidade 6k N . Sabendo-se que um alongamento de 14 m m e um
Uma linha de inclinação 4 : 10 é desenhada sobre uma placa de latão-amarelo de 150 m m de largura e 6,35m m de espessura. Usando a tabela apêndice B, para esse material, determinar a inclinação da lin
A barra de alumínio AD é ajustada a uma camisa, onde é aplicada uma pressão hidrostática de 40M P a , no trecho BC de comprimento igual a 300 m m . Sabendo-se que E = 70G P aev = 0,36 , determinar:A v