Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 13

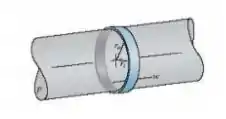
O anel cujas dimensões são mostradas na figura é colocado sobre uma membrana flexível bombeada com uma pressão p. Determine a mudança no raio interno do anel após a aplicação dessa pressão. O módulo de elasticidade para o anel é E.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que um anel num tubo tem uma membrana que é capaz de regular seu tamanho de acordo com a pressão p, e nos pede para calcular exatamente a diferença de raio. Viu?? Parece que é muita coisa, mas nem é tão difícil assim. Bora lá fazer?? Partiu??

Passo 2

Nosso primeiro passo será calcular a tensão circunferencial para o nosso anel, ou seja, só tendo o σ1.

σ 1 =   p r t =   p . r i r o -   r i  

Agora que sabemos quanto vale a nossa tensão circunferencial, vamos calcular quanto vale a força.

F =   σ 1   x   A =     p . r i r o -   r i   x   w   r o -   r i = w p r i

Passo 3

Pronto!! Com isso, podemos achar qual o deslocamento referente ao r i e, consequentemente, sua variação por causa da pressão p

δ r i   =   F . L A . E =   w   p   r i   r i w   r o -   r i   E =   p     r i ² r o -   r i   E

Resposta

δ r i   =   p     r i ² r o -   r i   E

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O olhal está sujeito à força de 250 N. Determine as tensões de tração e compressão máxima na seção a-a. A seção transversal é circular e tem 6 mm de diâmetro. Use a fórmula da viga curva para calcular
A tampa do tanque cilíndrico é parafusada ao tanque ao longo das abas. O tanque tem diâmetro interno de 1,5 m, e a espessura da parede é 18 mm. Se a pressão no interior do tanque for p = 1,20 MPa, det
O parafuso de prensa é composto pelos elementos estruturais AB e AC conectados por um pino em A. Se a força de compressão em C e B for 180 N, determine o estado de tensão no ponto F e indique os resul
Um pé-de-cabra é usado para retirar o prego em A. Se for necessária uma força de 40 N, determine as componentes da tensão na barra nos pontos D e E. Mostre os resultados em um elemento de volume difer
O parafuso de prensa exerce uma força de compressão de 2,5 kN nos blocos de madeira. Faça um rascunho da distribuição de tensão ao longo da seção a-a da prensa. Nesse lugar, a seção transversal é reta