Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 75
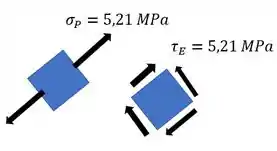
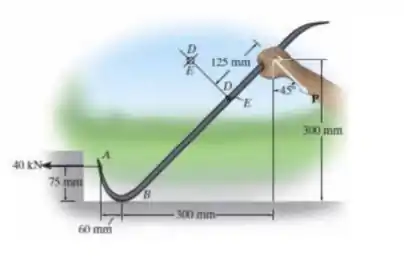
Um pé-de-cabra é usado para retirar o prego em A. Se for necessária uma força de 40 N, determine as componentes da tensão na barra nos pontos D e E. Mostre os resultados em um elemento de volume diferencial localizado em cada um desses pontos. A barra tem seção transversal circular com diâmetro de 12 mm. Não ocorre deslizamento em B.
Passo 1
Faaala aí galerinha do RespondeAí, tudo belezinha?!
Esse exercício aqui nos diz que um pé de cabra é usado para retirar o prego em , e sabendo que é necessária uma força de , ele nos pede para determinar as componentes da tensão na barra nos pontos e .
Vamos começar achando , para ter todas as informações. A gente pode fazer um DCL:
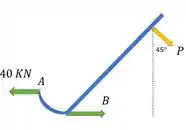
Como não há deslizamento e , ali há uma força de reação. Podemos achar pelo somatório de momentos em .
Passo 2
Cara, achando , a gente pode cortar nosso elemento na nossa seção e olhar só para um lado. O mais fácil é o lado direito que só tem . Fica assim:
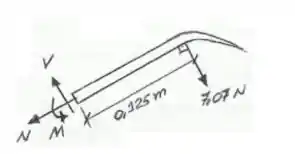
Repara que a gente colocou as componentes dos esforços internos da seção ali. Aí é só as achar pelas equações de equilíbrio.
Por somatório de forças:
E por somatório de momento
Passo 3
Agora vamos obter as tensões. Olha nossa seção (aqui os eixos foram arbitrados de forma que fica positivo e negativo).
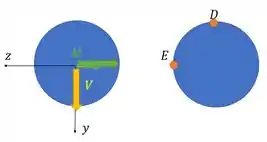
A flexão em E é zero por estar na linha neutra
Já a tensão cisalhante
Agora para D:
E sua tensão cisalhante é zero por estar na extremidade da peça.
Aí a gente faz nosso elemento assim. Lembrando que a tensão normal ficou positiva então ela sai da seção.
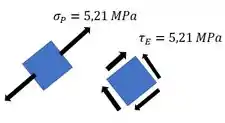
Resposta
