Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 7
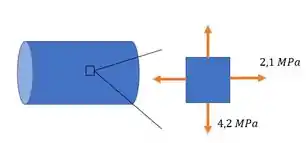
O tubo de extremidade aberta feito de cloreto de polivinil tem diâmetro interno de 100 mm e espessura de 5 mm e transportar água corrente à pressão de 0,42 MPa. Se esse fluxo no interior do tubo for interrompido devido ao fechamento de uma válvula, determine o estado de tensão nas paredes do tubo.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora.
Bom, nosso enunciado nos diz que o nosso tubo tem paredes com 5mm de espessura e 50 mm de raio interno.
Depois de falar isso tudo, ele nos pede tensão nas paredes, considerando que a água vem com uma pressão de 0,42 MPa e fica parada dentro do tubo, uma vez que fecharam o registro.
Vamos achar as tensões!
Passo 2
Nas questões de vasos cilíndricos de paredes finas, temos duas tensões normais nas paredes laterais do tubo: (na direção circunferencial, ou seja, do aro) e (no sentido longitudinal, ou seja, axial).
No nosso caso, sabemos que, como a extremidade foi fechada, teremos tanto a tensão axial quanto a circunferencial. Teremos a tensão que tende a esticar o comprimento da borda da seção circular do tubo do tubo, pela pressão que a água faz nas próprias paredes laterais:
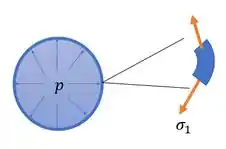
E teremos a tensão que faz com que o tubo tenda a ter suas paredes alongadas na horizontal. Porque? Como o tubo está fechado, a água vai fazer força nas bases do tubo cilindro. Essa força tende a causar essa tração longitudinal nas paredes laterais do tubo:
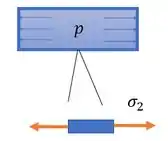
Então, podemos afirmar que as nossas tensões serão:
Passo 3
A gente pode calcular elas pelas fórmulinhas:
Agora para :
Passo 4
Aí a gente faz nosso elemento para ilustrar o estado de tensões do nosso tubo:
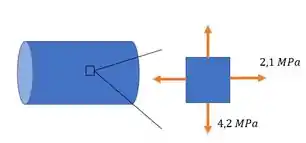
fica na direção longitudinal. E na direção do comprimento da seção circular.
Resposta
