Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 9

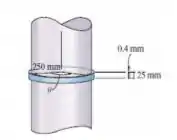
Inicialmente, a cinta de aço inoxidável 304 está perfeitamente ajustada em torno do cilindro rígido liso. Se ela for submetida a uma queda de temperatura não linear ΔT = 12sen²θ ºC, onde θ é dado em radianos, determine a tensão circunferencial na cinta.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?

Belezoca, nosso enunciado nos diz que a nossa cinta está certinha em volta de um cilindro rígido (ou seja, ele não vai mudar de tamanho quando sofrer a compressão ou a tração – guarda isso porque é MUITO importante) e que passou por uma queda de temperatura que segue aquela equação ali. Depois de falar isso tudo, ele nos pede tensão circunferencial. Bora lá fazer? Partiu?!

Passo 2

Como o nosso cilindro é rígido, temos que o deslocamento final vai ser igual ao deslocamento provocado pela variação da temperatura.

δ f =   δ t

F . L A . E =   ∫ 0 2 π α Δ T r d θ  

Logo:

F A 2 π r E a ç o =   α a ç o   r   ∫ 0 2 π Δ T d θ

Passo 3

Sendo assim, achamos que:

σ c =   α a ç o   .   E a ç o 2 π   ∫ 0 2 π Δ T d θ

σ c =   ( 17 × 10 - 6 ) ( 193 × 10 9 ) 2 π     ∫ 0 2 π 12 s e n ² θ d θ

σ c = 19,69   M P a

Resposta

σ c = 19,69   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O barril está cheio de água até em cima. Determine a distância s entre o aro superior e o aro inferior de modo que a força de tração em cada aro seja a mesma. Determine também a força em cada aro. O b
A cinta de aço A-36 tem 50 mm de largura e está presa ao redor do cilindro rígido. Se os parafusos forem apertados de modo que a tração neles seja 2 kN, determine a tensão normal na cinta, a pressão e
A figura mostra duas alternativas para apoiar o cilindro de parede fina. Determine o estado de tensão na parede do cilindro para ambas as alternativas, se o pistão P provocar uma pressão interna de 0,
Um tubo de madeira com diâmetro interno de 0,9 m é atado com aros de aço cuja área de seção transversal é 125 mm². Se a tensão admissível para os aros for σadm = 84 MPa, determine o espaçamento máximo
O tubo de extremidade aberta feito de cloreto de polivinil tem diâmetro interno de 100 mm e espessura de 5 mm. Se transportar água corrente à pressão de 0,42 MPa, determine o estado de tensão nas pare