Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 76
O anel de dimensão desprezível está submetido a uma força vertical de . Determine o maior comprimento da corda tal que a tração que atua em seja de . Além disso, qual é a força que atua na corda ? Dica: Use a condição de equilíbrio para determinar o ângulo para a fixação, depois determine usando a trigonometria aplicada a .
Passo 1
Fala, gente!
Para encontrarmos o valor da força e do comprimento , o equilíbrio de forças deve ser analisado nas duas dimensões e , pelo fato de as forças estarem atuando nelas.
Vamos fazer o diagrama de corpo livre tendo o ponto como origem para nos ajudar:
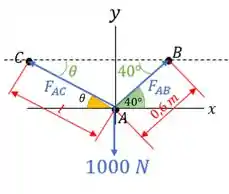
Aí a gente vai seguir o bizu do enunciado. Vamos primeiro achar e , sabendo que . E depois achar por trigonometria e pela geometria do problema.
Bora!
Passo 2
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
Adotando como positivo os sentidos para a direita (eixo ) e para cima (eixo ):
Tal que isolando :
Da mesma forma, para o eixo :
Passo 3
Agora, com as duas equações encontradas conseguimos montar um sistema de equações dado por:
Vamos substituir na segunda equação para obtermos:
E chegarmos em:
Substituindo o valor dado da tração na corda :
Aí a gente chega nessa equação
Essa equação a gente precisa de métodos numéricos para resolver, como não é o escopo da matéria, a gente vai jogar essa equação numa calculadora de equações (tem algumas online até), para achar o resultado, tá? Fica:
Voltando para a primeira equação do nosso sisteminha
Passo 4
Por fim, com o valor do ângulo, é possível utilizar a Lei dos Senos no triângulo ABC: