Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas Fundamentais - Ex. 1
Determine o momento da força em relação ao ponto .
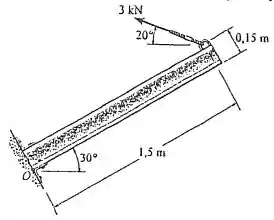
Passo 1
Para determinar o momento da força, é necessário determinar a distância do ponto até o ponto de atuação da força. Por conveniência, os eixos e serão considerados respectivamente ao longo da barra e perpendicularmente à ela como mostrado no diagrama de corpo livre a seguir:
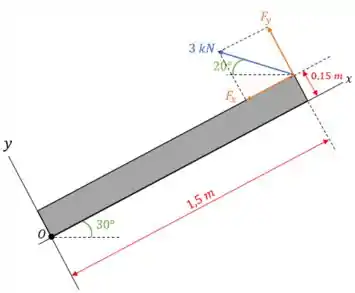
Logo, para a componente horizontal da força, a distância até o braço do momento será de:
E para a componente vertical será de:
Passo 2
Portanto, assumindo que os momentos positivos atuem no sentido anti-horário e lembrando que o momento gerado por uma força a uma distância do ponto de referência é dado por:
Então, temos que o momento da força em relação ao ponto é:
Tal que:
E, portanto, o momento terá o valor:
Resposta
Exercícios de Livros Relacionados
Se o homem em B exerce uma força P = 150N sobre sua corda, determine a intensidade da força F que o homem em C precisa exercer para impedir que o poste gire; ou seja, para que o momento resultante em
O cabo do martelo está sujeito à força F = 100N . Determine o momento dessa força em relação ao ponto A .
Para arrancar o prego em B , a força F exercida sobre o cabo do martelo precisa produzir um momento no sentido horário de 60N ∙ m em relação ao ponto A . Determine a intensidade necessária da força F
Dados os três vetores não nulos A , B e C , mostre que se A ∙ B × C = 0 , os três vetores necessitam estar no mesmo plano.
Se o momento produzido pela força de 4k N em relação ao ponto A é 10k N . m no sentido horário, determine o ângulo θ , onde 0 ° ≤ θ ≤ 90 ° .