Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 168
Pede-se: (a) Mostrar que a tensão em um canto de um membro retangular será nula, se a força vertical for aplicada num ponto localizado sobre a linha
(b) Mostrar também que se não ocorre tensão de tração no membro, é porque a força está aplicada em um ponto localizado dentro da área limitada pela linha: da parte e mais três similares correspondentes a condição de tensão nula em e D. (Esta área é conhecida como núcleo central da seção transversal.)
Passo 1
(a) Cara, o que ele quer é que a gente mostre que as coordenadas de satisfazem essa equação, quando a tensão em é .
E como a gente faz isso? Vamos achar a expressão para a tensão no ponto causada por essa força aí, beleza? Para esses eixos, a equação da tensão normal em um ponto para uma seção com uma força pontual aplicada é:
Lembrando que o sinal de menos fica no termo com o momento que causa compressão na parte positiva dos eixos.
Vamos montar ela. Bora!
Passo 2
Vamos calcular as características geométricas da seção:
Passo 3
Agora a gente calcula os esforços internos no centroide da seção, causados por . Temos essas componentes:
- Força axial entrando na seção:
- Momentos, de acordo com os eixos coordenados:
Passo 4
Agora é substituir tudo na fórmulinha, sabendo que . Fica assim:
Arrumando:
E daí temos que:
Olha só! Como queríamos provar!
Passo 5
(b) Para fazer essa a gente pode pensar o que significa no ponto termos tensão igual a zero: Significa que a linha neutra passa por esse ponto somente e só há compressão nessa seção, por causa da força pontual.
Acontece que se tem essa linha onde é aplicado, que faz a linha neutra passar pelo vértice . Há linhas similares que fazem o mesmo para todos os outros vértices da seção.
Vamos localizar nossa linha na seção. Pela figura (e pela equação), ela passa pelos pontos:
Passo 6
Bora colocar ela na seção e analisar. A nossa linha é essa tracejada. Se for aplicada sobre ela, a tensão em zera.
Mas se ela for aplicada na área amarela, no ponto vai aparecer uma tração (por causa do momento) e se for aplicada na parte azul, terá compressão.
Queremos que em só haja compressão, então nossa força só pode ser aplicada na área azul.
E gente sabe que existe uma linha semelhante a do item (a) para todos os vértices, dividindo a seção em uma área onde deve ser aplicada para que só haja compressão e numa que vai causar tração, para cada um desses vértices.
Se a gente fizer a interseção entre a áreas onde pode ser aplicado para que só haja compressão nos vértices (baseado nas localizações das retas semelhantes a do item (a)), temos:
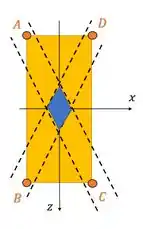
Para só ocorrer compressão em todos os vértices, nossa força precisa ser aplicada nesse losango azul. Aí é exatamente a região que ele chama de núcleo central.
Se em todos os vértices só há compressão, significa que não há tração nenhuma na seção causada por . E isso é o que ele pede para provar! Arrasamos!
Resposta
Prova nos passos