Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 167
Em uma dada seção de um perfil laminado de aço , o efeito da gravidade é representado por um vetor-momento , Expressando por a máxima tensão na viga quando , determinar o ângulo de inclinação da viga para que a máxima tensão seja .
Passo 1
Primeiro, vamos olhar numa tabelinha os dados desse perfil:
- Momentos de Inércia:
- Dimensões:
A parada é a gente encontrar uma expressão para essa tensão máxima , e dizer que um terço dela deve valer a tensão máxima quando o ângulo é zero:
Bora!
Passo 2
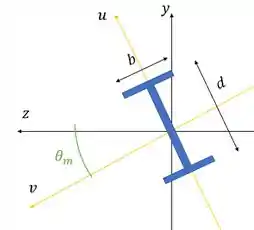
Agora a gente tem que descobrir onde é a linha neutra. Isso porque a tensão máxima ocorre nos pontos mais distantes dela. A gente pode lembrar que essa linha está sempre entre o eixo da direção do momento e o eixo de menor momento de inércia .
Por isso, podemos supor que a linha neutra está nessa posição:
Vemos que os pontos mais distantes da nossa linha neutra são e . Eles terão as tensões máximas.
Passo 3
Vamos usar a relação de tensão no ponto , já que a distância entre a linha neutra e ele é semelhante à distância entre a linha neutra e . Ela vai ter essa carinha:
Vamos projetar o nosso momento , que está na direção do eixo , nos eixos principais:
E achar e .
Passo 4
Agora a gente pode usar:
Lembrando que:
Aí substituindo tudo, fica:
Agora é resolver isso para . Como é uma conta muito feinha. A gente vai usar um software para resolver. Aí é substituir os dados e jogar no nosso programinha. Achamos: