Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 123

Para que seja possível a entrada no interior de um tubo de seção quadrada de 6,35 m m de espessura, a porção B D de um dos lados do tubo foi removida. Sabendo-se que o carregamento no tubo é equivalente a duas forças axiais, iguais e apostas, de 70   k N , atuando no centro geométrico A   e   E das extremidades do tubo, determinar:

  1. A máxima tensão na seção a - a
  2. A tensão no ponto F .

D a d o s :   O   c e n t r ó i d e   d a   s e ç ã o   t r a n s v e r s a l   é   o   p o n t o   C   e   I   =   2   x   10 6   m m 4 .

Passo 1

Nossos objetivos são dois, determinar a máxima tensão e a tensão no ponto F, sabemos que a fórmula da tensão é dada por:

σ x = P A - M y I

Sabemos pelo enunciado que:

P = 70   k N = 70000   N

O momento precisamos da excentricidade, que é dada por:

e = - 50 - 36,3 = - 13,7   m m

M = P . e

M = 70000   . - 13,7 = - 959000   N m m

O momento de inércia e as áreas são:

I   =   2   x   10 6   m m 4

A = 100   x   6,35 + 2 x 6,35 x 100 - 6,35 = 1824,355   m m 2

Passo 2

Para o item A) queremos a máxima tensão que age na seção, para isso teremos que pegar o Y, sendo assim teremos que:

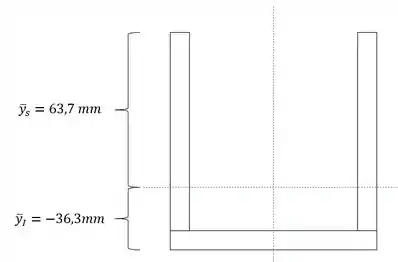
Como o momento fletor é negativo, precisamos do y positivo para termos a máxima tensão, que nesse caso é de tração, sendo assim, termos que:

σ M á x = P A - M y I = 70000 1824,355 - - 959000   .     63,7 2   x   10 6 = 68,9 N m m 2 = 68,9   M P a

E para calcular a tensão no ponto F, precisamos do y negativo, dessa maneira, teremos que:

σ F = P A - M y I = 70000 1824,355 - - 959000   .     - 36,3 2   x   10 6 = 20,9 6 N m m 2 = 20,9 6   M P a

Resposta

  1. σ M á x = 68,9   M P a

  2. σ F = 20,96   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As quatro barras mostradas tem a seção transversal de mesma área. Para os carregamentos dados, mostrar que para estas barras: (a) as máximas tensões de compressão obedecem à proporção 4:5:7:9; (b) as
Um sensor de deformação localizado no ponto A indica uma deformação de – 400 x 10 - 6 mm/mm, quando um momento M é aplicado á viga de aço mostrada. Sabendo-se que M atua em um plano vertical e usando
O momento M atua em um plano vertical e está aplicado a uma viga orientada como mostrado. Determinar: (b) a máxima tensão de tração na viga.
O momento M é aplicado a uma viga de seção transversal mostrada, em um plano formando um ângulo β com a vertical. Determinar: (c) o ângulo que a linha neutra forma com o plano horizontal.
O momento M atua em um plano vertical e está aplicado a uma viga orientada como mostrado. Determinar: (a) o ângulo que o eixo neutro forma com o plano horizontal.