Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 154
O ângulo da superfície de suporte em C pode variar de 0 (vertical) a 90∘ (horizontal).
(a) Trace a força no membro BC como uma função de θ neste intervalo. Observe quaisquer condições incomuns.
(b) Para qual valor de θ, se houver, a força no membro BC é zero?
(c) Se o membro BC for projetado para falhar com uma carga de 1000 lb em tensão ou compressão, qual é o intervalo permitido para o ângulo θ?
Passo 1
(a) Primeiro, podemos analisar a junta A para determinar as forças nos membros AC
Observe que as forças nos membros AB e AC são constantes para qualquer valor de θ, uma vez que a mudança do ângulo não os afeta.
Observe também que assumiremos que todos os membros desconhecidos estão em tensão
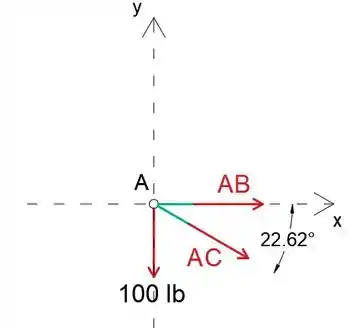
Aplicando as equações de equilíbrio, determinaremos a força nos membros AC
Como obtivemos o resultado negativo, isso significa que o membro está em compressão
Passo 2
Agora podemos analisar a junta C.
Observe que criamos o sistema de coordenadas mOn, onde o eixo m é paralelo ao membro BCD, a fim de facilitar os cálculos.
Observe também que assumimos que todos os membros desconhecidos estão sob tensão, portanto, os membros estarão em compressão quando seu valor for negativo.
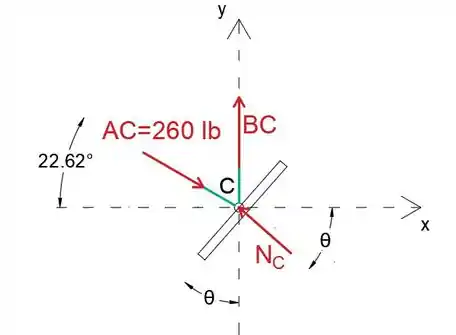
Equacionando a soma das forças na direção x a zero, podemos determinar a força de reação NC
Equacionando a soma das forças na direção y a zero, podemos determinar a força BC
Substitua NC pela expressão (1)
Usando uma calculadora gráfica como o Desmos, traçaremos a função fornecida para o CD
Podemos ver que o membro está em compressão (valor negativo) e a força de compressão mínima do membro CD é:
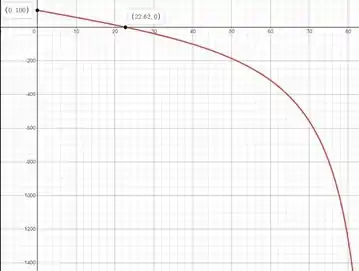
Passo 3
(b) Quando a força de reação em C é paralela à força do membro AC, essas duas forças serão iguais e em equilíbrio por si mesmas, portanto a força BC deve ser igual a zero quando a força de reação em C é paralela à força do membro AC , ou seja, em θ = 22,62∘
Passo 4
Observe que o sistema irá falhar quando BC = 1000 ou BC = -1000lb (onde o sinal “-” representa compressão e “ + "sinal de tensão), então, a fim de determinar o intervalo de θ para o qual a treliça não entrará em colapso, podemos ler o ângulo do gráfico na etapa 5 ou substituir BC por 1000 e -1000 na equação (2).
Podemos ver no gráfico que a treliça entrará em colapso em θ = 77,692∘, então o intervalo permitido para θ é:
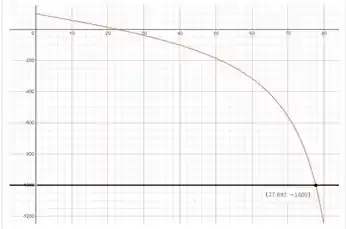
Resposta
(a)
Em θ = 90 ∘ a treliça não é estável
(b)
(c)